已知:关于x的一元二次方程mx2-(2m+2)x+m-1=0
(1)若此方程有实根,求m的取值范围;
(2)在(1)的条件下,且m取最小的整数,求此时方程的两个根;
(3)在(2)的前提下,二次函数y=mx2-(2m+2)x+m-1与x轴有两个交点,连接这两点间的线段,并以这条线段为直径在x轴的上方作半圆P,设直线l的解析式为y=x+b,若直线l与半圆P只有两个交点时,求出b的取值范围.

解:(1)∵关于x的一元二次方程有实根∴m≠0,且△≥0
∴△=(2m+2)
2-4m(m-1)=12m+4≥0
解得m≥
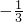
∴当m≥
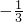
,且 m≠0时此方程有实根;
(2)∵在(1)的条件下,当m取最小的整数,
∴m=1
∴原方程化为:x
2-4x=0
x(x-4)=0
x
1=0,x
2=4
(3)解:如图所示:①当直线l经过原点O时与半圆P有两个交点,即b=0
②当直线l与半圆P相切于D点时有一个交点,如图由题意可得Rt△EDP、Rt△ECO是等腰直角三角形,
∵DP=2∴EP=
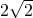
….(6分)
∴OC=
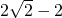
即b=
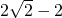
∴当0≤b<
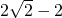
时,直线l与半圆P只有两个交点.
分析:(1)根据关于x的一元二次方程有实根得m≠0,且△≥0从而得到12m+4≥0求得m的取值范围即可;
(2)在(1)的条件下,当m取最小的整数时m=1,于是原方程化为:x
2-4x=0,解得即可;
(3)根据当直线l经过原点O时与半圆P有两个交点,即b=0,当直线l与半圆P相切于D点时有一个交点时得到b=
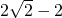
,从而得到当0≤b<
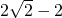
时,直线l与半圆P只有两个交点.
点评:本题具有较强的综合性,考查了一元二次方程的根的情况,二次函数与对应的一元二次方程的联系,讨论一次函数与半圆的交点的情况.

 解:(1)∵关于x的一元二次方程有实根∴m≠0,且△≥0
解:(1)∵关于x的一元二次方程有实根∴m≠0,且△≥0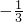
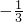 ,且 m≠0时此方程有实根;
,且 m≠0时此方程有实根;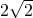 ….(6分)
….(6分)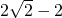 即b=
即b=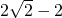
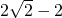 时,直线l与半圆P只有两个交点.
时,直线l与半圆P只有两个交点.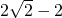 ,从而得到当0≤b<
,从而得到当0≤b<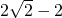 时,直线l与半圆P只有两个交点.
时,直线l与半圆P只有两个交点.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案