
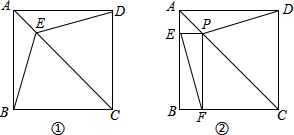
 如图①,在正方形ABCD中,点E在AC上.
如图①,在正方形ABCD中,点E在AC上.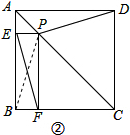 (1)证明:在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,
(1)证明:在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,
|


科目:初中数学 来源: 题型:
 在“我喜欢的体育项目”调查活动中,小亮调查了自己所在班级48人,调查时,喜欢打篮球的记为A,喜欢踢足球的记为B,喜欢游泳的记为C,喜欢跑步的记为D,记录结果如下:
在“我喜欢的体育项目”调查活动中,小亮调查了自己所在班级48人,调查时,喜欢打篮球的记为A,喜欢踢足球的记为B,喜欢游泳的记为C,喜欢跑步的记为D,记录结果如下:| 喜欢的项目 | 总人数/人 |
| 打篮球(A) | |
| 踢足球(B) | |
| 游泳(C) | |
| 跑步(D) |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com