
分析 (1)①甲方式购买和包装x吨农产品所需资金为:4x万元;乙方式购买和加工其余农产品所需资金为:3(20-x)+3(20-x)+12=(132-6x)万元;
②当2≤x<8时,当x≥8时,分别列出函数解析式即可;
③当2≤x<8时,列方程得到-x2+7x+48=48,解得x1=7,x2=0(不合题意);当x≥8时,-x+48=48,解得x=0.得到当毛利润达到48万元时,甲种方式销售7吨;
④由题意可知,当x=8时,利润最小为40万元.
(2)本问是方案设计问题,总投入为132万元,这笔132万元包括购买农产品的费用+甲方式农产品加工成本+乙方式农产品加工成本.①其中甲方式经销农产品x吨,则总经销量p为-x+14吨,②共购买了m吨农产品,其中甲方式农产品为x吨,乙方式农产品为(m-x)吨,分别求出当2≤x<8时及当x≥8时w关于x的表达式,并分别求出其最大值.
解答 解:(1)①甲方式购买和包装x吨农产品所需资金为:4x万元;
乙方式购买和加工其余农产品所需资金为:3(20-x)+3(20-x)+12=(132-6x)万元;
故答案为:4x,(132-6x);
②当2≤x<8时,
w甲=x(-x+14)-x=-x2+13x;
w乙=9(20-x)-[12+3(20-x)]=108-6x
∴w=w甲+w乙-3×20
=(-x2+13x)+(108-6x)-60
=-x2+7x+48;
当x≥8时,
w甲=6x-x=5x;
w乙=9(20-x)-[12+3(20-x)]=108-6x
∴w=w甲+w乙-3×20
=(5x)+(108-6x)-60
=-x+48.
③当2≤x<8时,-x2+7x+48=48,解得x1=7,x2=0(不合题意);
当x≥8时,-x+48=48,解得x=0.
∴当毛利润达到48万元时,甲种方式销售7吨.
④由题意可知,当x=8时,利润最小为40万元.
(2)设该公司用132万元共购买了m吨农产品,其中甲方式购买x吨,乙方式购买(m-x)吨,
则购买费用为3m万元,甲方式农产品加工成本为x万元,乙方式农产品加工成本为[12+3(m-x)]万元,
∴3m+x+[12+3(m-x)]=132,化简得:x=3m-60.
①当2≤x<8时,
wA=x(-x+14)-x=-x2+13x;
wB=9(m-x)-[12+3(m-x)]=6m-6x-12
∴w=wA+wB-3×m
=(-x2+13x)+(6m-6x-12)-3m
=-x2+7x+3m-12.
将3m=x+60代入得:w=-x2+8x+48=-(x-4)2+64
∴当x=4时,有最大毛利润64万元,
此时m=$\frac{64}{3}$,m-x=$\frac{52}{3}$;
②当x≥8时,
w甲=6x-x=5x;
w乙=9(m-x)-[12+3(m-x)]=6m-6x-12
∴w=w甲+w乙-3×m
=(5x)+(6m-6x-12)-3m
=-x+3m-12.
将3m=x+60代入得:w=48
∴当x>8时,有最大毛利润48万元.
综上所述,购买农产品共$\frac{64}{3}$吨,其中甲方式农产品4吨,乙方式农产品$\frac{52}{3}$吨,公司能够获得最大毛利润,最大毛利润为64万元.
点评 本题考查了二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.涉及到分段函数时,注意要分类讨论.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:解答题
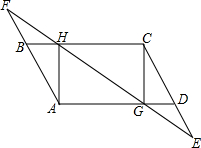 如图,分别延长平行四边形ABCD的边CD、AB到E、F,使DE=BF=$\frac{1}{2}$CD,连接EF,分别交AD,BC于G,H,连接CG,AH
如图,分别延长平行四边形ABCD的边CD、AB到E、F,使DE=BF=$\frac{1}{2}$CD,连接EF,分别交AD,BC于G,H,连接CG,AH查看答案和解析>>
科目:初中数学 来源: 题型:填空题
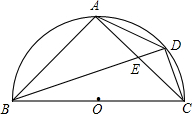 如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.
如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,AB=$\sqrt{2}$,BC=$\sqrt{3}$,点E是边CD延长线上一点,且DE=1,将△ADE绕点A顺时针旋转后,点E落在直线BC上,则旋转度数是( )
如图,矩形ABCD中,AB=$\sqrt{2}$,BC=$\sqrt{3}$,点E是边CD延长线上一点,且DE=1,将△ADE绕点A顺时针旋转后,点E落在直线BC上,则旋转度数是( )| A. | 30° | B. | 45° | C. | 45°或135° | D. | 75°或165° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
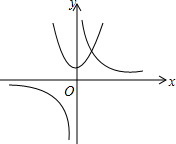 请阅读下列内容:我们在平面直角坐标系中画出抛物线y=x2+1和双曲线y=$\frac{2}{x}$,如图所示,利用两图象的交点个数和位置来确定方程x2+1=$\frac{2}{x}$有一个正实数根,这种方法称为利用的图象判断方程根的情况请用图象法判断方程-(x-3)2+4=$\frac{2}{x}$的根的情况两个正根一个负根(填写根的个数及正负).
请阅读下列内容:我们在平面直角坐标系中画出抛物线y=x2+1和双曲线y=$\frac{2}{x}$,如图所示,利用两图象的交点个数和位置来确定方程x2+1=$\frac{2}{x}$有一个正实数根,这种方法称为利用的图象判断方程根的情况请用图象法判断方程-(x-3)2+4=$\frac{2}{x}$的根的情况两个正根一个负根(填写根的个数及正负).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
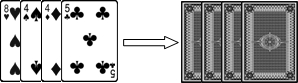
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com