
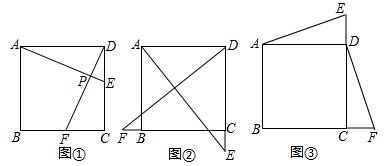
分析 (1)先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;
(2)由正方形的性质得出AD=DC,∠ADE=∠DCF=90°,DE=CF,SAS证出△ADE≌△DCF,得出AE=DF,∠DAE=∠CDF,证出∠DAE+∠ADF=90°,得出AE⊥DF;
(3)由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF.
解答 解:(1)AE=DF,AE⊥DF;理由如下:
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠C=90°,
在△ADE和△DCF中,$\left\{\begin{array}{l}{AD=DC}&{\;}\\{∠ADC=∠C}&{\;}\\{DE=CF}&{\;}\end{array}\right.$,
∴△ADE≌△DCF(SAS),
∴AE=DF,∠DAE=∠CDF,
由于∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°,
∴∠APD=90°,
∴AE⊥DF;
故答案为:AE=DF,AE⊥DF;
(2)是;理由如下:
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠DCF=90°,
在△ADE和△DCF中,$\left\{\begin{array}{l}{AD=DC}&{\;}\\{∠ADC=∠C}&{\;}\\{DE=CF}&{\;}\end{array}\right.$,
∴△ADE≌△DCF(SAS),
∴AE=DF,∠DAE=∠CDF,
∵∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°,
∴AE⊥DF;
(3)成立;理由如下: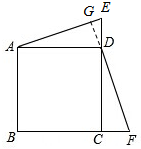 同(1)得:AE=DF,∠DAE=∠CDF,
同(1)得:AE=DF,∠DAE=∠CDF,
延长FD交AE于点G,如图所示:
则∠CDF+∠ADG=90°,
∴∠ADG+∠DAE=90°,
∴∠AGD=90°,
∴AE⊥DF.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、互余两角的关系、垂线的证法等知识;本题难度较大,综合性强,熟练掌握正方形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
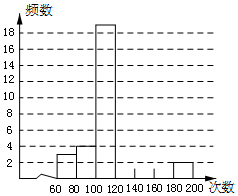 校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:
校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:| 次数分组 | 频数 |
| 60≤x<80 | 3 |
| 80≤x<100 | 4 |
| 100≤x<120 | 19 |
| 120≤x<140 | 10 |
| 140≤x<160 | 8 |
| 160≤x<180 | 4 |
| 180≤x<200 | 2 |
| 合计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
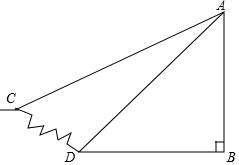 如图,某同学自某观景平台AB上的A处看到有一个11阶的楼梯,他测得最上面楼梯角C的俯角为40°,最下面楼梯角D的俯角为45°,若每个台阶的高为15cm,宽为30cm,试求观景平台的高AB(同学身高忽略不计).(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,$\sqrt{2}≈1.41$)
如图,某同学自某观景平台AB上的A处看到有一个11阶的楼梯,他测得最上面楼梯角C的俯角为40°,最下面楼梯角D的俯角为45°,若每个台阶的高为15cm,宽为30cm,试求观景平台的高AB(同学身高忽略不计).(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,$\sqrt{2}≈1.41$)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球的次数n | 200 | 300 | 400 | 500 | 800 | 1000 |
| 摸到白球的次数m | 117 | 186 | 242 | 296 | 483 | 599 |
| 摸到白球的频率 $\frac{n}{m}$ | 0.585 | 0.620 | 0.605 | 0.592 | 0.604 | 0.599 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
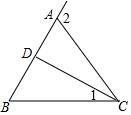 已知∠2是△ABC的一个外角,那么∠2与∠B+∠1的大小关系是( )
已知∠2是△ABC的一个外角,那么∠2与∠B+∠1的大小关系是( )| A. | ∠2>∠B+∠1 | B. | ∠2=∠B+∠1 | C. | ∠2<∠B+∠1 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查市场上老酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了违禁品 | |
| D. | 调查某市初中生的睡眠情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
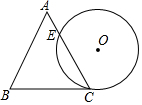 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )| A. | 4cm | B. | 3cm | C. | $\frac{2\sqrt{3}π}{3}$cm | D. | $\frac{\sqrt{3}π}{3}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com