
����Ŀ��������ĸ�ľ����β�����������������ݶ����ӣ����ܹ���һ��ƽ��ͼ�Σ� 
��1�����̶�����ľ��AB��BC��AD������AB=AD=2cm��BC=5cm����ͼ�����õ��ĸ�ľ��CD=5cm���жϴ�ʱ��B���D�Ƿ���ȣ���˵�����ɣ�
��2�����̶�һ��ľ��AB������AB=2cm������ľ��CD=5cm�����ľ��AD��BC�ij��Ȳ��䣬����D�Ƶ�BA���ӳ�����ʱ����CҲ��BA���ӳ����ϣ�����C�Ƶ�AB���ӳ�����ʱ����A��C��D�ܹ����ܳ�Ϊ30cm�������Σ����ľ��AD��BC�ij��ȣ�
���𰸡�
��1���⣺��ȣ�
���ɣ�����AC��
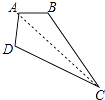
�ڡ�ACD�͡�ACB�У�
�� 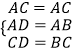 ��
��
���ACD�ա�ACB��SSS����
���B=��D
��2���⣺��AD=x��BC=y��
�ߵ���C�ڵ�D�Ҳ�ʱ�� ![]() �����
����� ![]() ��
��
����C�ڵ�D���ʱ�� ![]() �����
����� ![]() ��
��
��ʱAC=17��CD=5��AD=8��5+8��17��
������⣬
��AD=13cm��BC=10cm��
����������1������AC������SSS֤������������ȫ�ȼ��ɣ���2�����������ٵ���C�ڵ�D�Ҳ�ʱ���ڵ���C�ڵ�D���ʱ���ֱ��г������鼴�ɽ�����⣬ע������������������߹�ϵ�����������Ƿ�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������A(��3��4)��B(��3��0)��C(��1��0) .��DΪ�����������y = ax2+bx+c����B. ����P�ӵ�D��������DC�����C�˶���ͬʱ����Q�ӵ�B��������BA�����A�˶�����P��Q�˶����ٶȾ�Ϊÿ��1����λ���˶���ʱ��Ϊt��. ����P��PE��CD��BD�ڵ�E������E��EF��AD�ڵ�F�����������ڵ�G.

��1���������ߵĽ���ʽ��
��2����tΪ��ֵʱ���ı���BDGQ�����������ֵΪ���٣�
��3������P��Q�˶������У��ھ���ABCD�ڣ�������߽磩�Ƿ���ڵ�H��ʹ��B��Q��E��HΪ������ı��������Σ������ڣ���ֱ��д����ʱ���ε��ܳ����������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABΪֱ������Բ��O����BC�ڵ�D������AD������D��DE��AC������Ϊ��E����AB���ӳ����ڵ�F��
��1����֤��EF�ǡ�O�����ߣ�
��2����֤����FDB�ס�FAD��
��3�������O�İ뾶Ϊ5��sin��ADE=![]() ����BF�ij���
����BF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������6����ֱ�д��1��2��3��4��5��6���������аڷŵ������������ôÿ���������ϵ����Ǽ��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=15��AC=12��BC=9��������C�����AB���еĶ�Բ��CB��CA�ֱ��ཻ�ڵ�E��F�����߶�EF���ȵ���Сֵ��__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㣬��ȷ���ǣ�������
A. x3x2��x6B. 5x3��3x3��2x3
C. ��x5��2��x7D. ��x��y��2��x2��y2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��������һ�����������������ĺ�Ϊ������������һ����Ϊ�����������һ���������Ļ�Ϊ���������������������Ļ�Ϊ�㣮�ɴ˿ɵã����ax��b��0������a��bΪ��������xΪ����������ôa��0��b��0����������֪ʶ������������⣺
��1�������a��2��![]() ��b��3��0������a��bΪ����������ôa��______________��
��b��3��0������a��bΪ����������ôa��______________��
��2�������2��![]() ��a����1��
��a����1��![]() ��b��5������a��bΪ����������a��2b��ֵ��
��b��5������a��bΪ����������a��2b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ֲ���ʵ������ֻ��0.000000076�ˣ���0.000000076�ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com