
分析 (1)先将题目中的式子化简,然后根据(x2+mx+1)(x2-2x+n)的展开式中不含x2和x3项,可以求得m、n的值;
(2)先化简题目中的式子,然后将m、n的值代入化简后的式子即可解答本题.
解答 解:(1)(x2+mx+1)(x2-2x+n)
=x4-2x3+nx2+mx3-2mx2+mnx+x2-2x+n
=x4+(-2+m)x3+(n-2m+1)x2+(mn-2)x+n,
∵(x2+mx+1)(x2-2x+n)的展开式中不含x2和x3项,
∴$\left\{\begin{array}{l}{-2+m=0}\\{n-2m+1=0}\end{array}\right.$,得$\left\{\begin{array}{l}{m=2}\\{n=3}\end{array}\right.$,
即m的值为2,n的值为3;
(2)(m+2n+1)(m+2n-1)+(2m2n-4mn2+m3)÷(-m)
=[(m+2n)+1][(m+2n)-1]-2mn+4n2-m2
=(m+2n)2-1-2mn+4n2-m2
=m2+4mn+4n2-1-2mn+4n2-m2
=2mn+8n2-1,
当m=2,n=3时,
原式=2×2×3+8×32-1=83.
点评 本题考查整式的混合运算--化简求值,解题的关键是明确整式化简求值的方法.


科目:初中数学 来源: 题型:解答题
 △ABC在平面直角坐标系xOy中的位置如图所示:
△ABC在平面直角坐标系xOy中的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
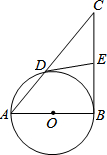 已知:如图,以Rt△ABC的边AB为直径的⊙O交斜边AC于点D,E是BC边的中点,连接DE.
已知:如图,以Rt△ABC的边AB为直径的⊙O交斜边AC于点D,E是BC边的中点,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com