
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点. 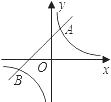
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
【答案】
(1)解:∵A(1,3)在y= ![]() 的图象上,
的图象上,
∴k=3,∴y= ![]() .
.
又∵B(n,﹣1)在y= ![]() 的图象上,
的图象上,
∴n=﹣3,即B(﹣3,﹣1)
∴ ![]()
解得:m=1,b=2,
∴反比例函数的解析式为y= ![]() ,一次函数的解析式为y=x+2
,一次函数的解析式为y=x+2
(2)解:从图象上可知,当x<﹣3或0<x<1时,反比例函数的值大于一次函数的值.
【解析】(1)反比例函数y= ![]() 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点,把A点坐标代入反比例函数解析式,即可求出k,得到反比例函数的解析式.将B(n,﹣1)代入反比例函数的解析式求得B点坐标,然后再把A、B点的坐标代入一次函数的解析式,利用待定系数法求出一次函数的解析式;(2)根据图象,分别在第一、三象限求出反比例函数的值大于一次函数的值时x的取值范围.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点,把A点坐标代入反比例函数解析式,即可求出k,得到反比例函数的解析式.将B(n,﹣1)代入反比例函数的解析式求得B点坐标,然后再把A、B点的坐标代入一次函数的解析式,利用待定系数法求出一次函数的解析式;(2)根据图象,分别在第一、三象限求出反比例函数的值大于一次函数的值时x的取值范围.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD. 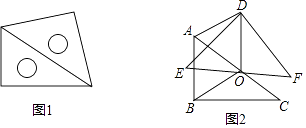
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l:y=(x﹣h)2﹣4(h为常数)
(1)如图1,当抛物线l恰好经过点P(1,﹣4)时,l与x轴从左到右的交点为A、B,与y轴交于点C.
①求l的解析式,并写出l的对称轴及顶点坐标.
②在l上是否存在点D,使S△ABD=S△ABC , 若存在,请求出D点坐标,若不存在,请说明理由.
③点M是l上任意一点,过点M做ME垂直y轴于点E,交直线BC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点M的坐标.
(2)设l与双曲线y= ![]() 有个交点横坐标为x0 , 且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
有个交点横坐标为x0 , 且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1 , 得∠A1;∠A1BC和∠A1CD的平分线交于点A2 , 得∠A2;…∠A2016BC和∠A20l6CD的平分线交于点A2017 , 则∠A2017=°. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积为( ) 
A.5
B.10
C.15
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(1)被抽样调查的学生有 ________人,并补全条形统计图;
(2)每天户外活动时间的中位数是________ (小时);
(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有________人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com