
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
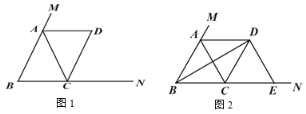
(1)如图 1,求证:四边形 ABCD 是平行四边形;
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
【答案】(1)见解析;(2)△ABC、△DBC、△ABD、△ACD.
【解析】
(1)根据等腰三角形的性质和三角形外角的性质可得∠CAM=2∠ABC,根据角平分线的定义可得∠CAM=2∠MAD,等量代换得到∠ABC=∠MAD,进而证得AD∥BC即可解决问题;
(2)首先证明平行四边形ABCD是菱形,然后证明△DCE是等边三角形,得到CE=CD=BC=AD,根据等底等高的三角形面积相等可得答案.
解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∴∠CAM=∠ABC+∠ACB=2∠ABC,
∵AD是∠CAM 的平分线,
∴∠CAM=2∠MAD,
∴∠ABC=∠MAD,
∴AD∥BC,
∵CD∥AB,
∴四边形ABCD是平行四边形;
(2)∵∠ABC=60°,AB=AC,四边形ABCD是平行四边形,
∴△ABC是等边三角形,∠DCE=∠ABC=60°,
∴AB=BC,
∴平行四边形ABCD是菱形,
∴∠DBE=30°,
∵DE⊥BD,
∴∠DEB=60°,
∴△DCE是等边三角形,
∴CE=CD=BC=AD,
∵AD∥BC,
∴△ABC、△DBC、△ABD、△ACD的面积都与△CDE的面积相等.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】2018年9月17日世界人工智能大会在.上海召开,人工智能的变革力在教育、制造等领域加速落地.在某市举办的一次中学生机器人足球赛中,有四个代表队进入决赛,决赛中,每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛),以下是积分表的一-部分.
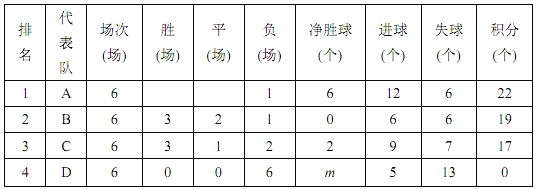
(说明:积分=胜场积分十平场积分+负场积分)
(1)D代表队的净胜球数m=______;
(2)本次决赛中,胜一场积______分,平一场积______分,负一场积_______分;
(3)此次竞赛的奖金分配方案为:进入决赛的每支代表队都可以获得参赛奖金6000元;另外,在决赛期间,每胜一场可以再获得奖金2000元,每平一场再获得奖金1000元.请根据表格提供的信息,求出冠军A队一共能获得多少奖金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在矩形ABCD中,AB=2AD,E为CD的中点,则∠AEB ∠ACB(填“>”“<”“=”);
问题探究
(2)如图②,在正方形ABCD中,P为CD边上的一个动点,当点P位于何处时,∠APB最大?并说明理由;
问题解决
(3)如图③,在一幢大楼AD上装有一块矩形广告牌,其侧面上、下边沿相距6米(即AB=6米),下边沿到地面的距离BD=11.6米.如果小刚的睛睛距离地面的高度EF为1.6米,他从远处正对广告牌走近时,在P处看广告效果最好(视角最大),请你在图③中找到点P的位置,并计算此时小刚与大楼AD之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟于中秋节前![]() 天里销售某品牌月饼,其进价为
天里销售某品牌月饼,其进价为![]() 元/
元/![]() .设第
.设第![]() 天的销售价格为
天的销售价格为![]() (元/
(元/![]() )销售量为
)销售量为![]() .该超市根据以往的销售经验得出以下的销售规律:①与
.该超市根据以往的销售经验得出以下的销售规律:①与![]() 满足一次函数关系,且当
满足一次函数关系,且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .②
.②![]() 与
与![]() 的关系为
的关系为![]() .
.
(1)![]() 与
与![]() 的关系式为________;
的关系式为________;
(2)当![]() 时,求第几天的销售利润
时,求第几天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)若在当天销售价格的基础上涨![]() 元/
元/![]() ,在第
,在第![]() 天至
天至![]() 天销售利润最大值为
天销售利润最大值为![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为疫情期间表现优秀的学生购买奖品.已知购买![]() 个
个![]() 奖品和
奖品和![]() 个
个![]() 奖品共需
奖品共需![]() 元;购买
元;购买![]() 个
个![]() 奖品和
奖品和![]() 个
个![]() 奖品共需
奖品共需![]() 元
元
(1)求![]() 两种奖品的单价;
两种奖品的单价;
(2)学校准备购买![]() 两种奖品共
两种奖品共![]() 个,且
个,且![]() 奖品的数量不少于
奖品的数量不少于![]() 奖品数量的一半,请设计出最省钱的购买方案,并说明理由.
奖品数量的一半,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一小长假前夕,某服装店的老板到服装厂购买男士夏装和女士夏装.已知购进![]() 套男士夏装和
套男士夏装和![]() 套女士夏装需要
套女士夏装需要![]() 元;购进
元;购进![]() 套男士夏装和
套男士夏装和![]() 套女士夏装需要
套女士夏装需要![]() 元.
元.
(1)求男士夏装和女士夏装每套进价分别是多少元;
(2)若![]() 套男士夏装的售价为
套男士夏装的售价为![]() 元,
元,![]() 套女士夏装的售价为
套女士夏装的售价为![]() 元,时装店决定购进男士夏装的数量为女士夏装的数量的
元,时装店决定购进男士夏装的数量为女士夏装的数量的![]() 还多
还多![]() 套,如果购进的男士夏装和女士夏装全部售出后的总利润超过
套,如果购进的男士夏装和女士夏装全部售出后的总利润超过![]() 元,那么此次至少可购进多少套女士夏装?
元,那么此次至少可购进多少套女士夏装?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】诗词是中华民族灿烂文化中的瑰宝,王老师连续三个月在班上开展针对全班同学的古诗词默写的测试活动.如图,王老师将三次默写的成绩(满分10分)做了统计,并绘制了折线统计图.由图可知,以下结论错误的是( )
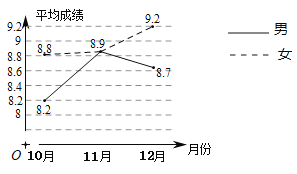
A.男、女生11月份的平均成绩相同
B.10月到12月,女生的平均成绩一直在进步
C.10月到11月,女生的平均成绩的增长率约为8.5%
D.11月到12月女生的平均成绩比10月到11月的增长快
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com