
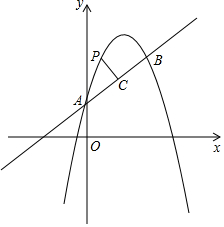
 如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+1交于A、B两点,其中点A在y轴上,点B的横坐标是4,P为抛物线上一动点,过点P作PC⊥AB,垂足为点C,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+1交于A、B两点,其中点A在y轴上,点B的横坐标是4,P为抛物线上一动点,过点P作PC⊥AB,垂足为点C,设点P的横坐标为m.分析 (1)求出A、B两点坐标代入抛物线的解析式即可解决问题.
(2)作PF⊥x轴于F,交AB于E,直线AB交x轴于D.设P(m,-m2+$\frac{9}{2}$m+1),则E(m,$\frac{1}{2}$m+1),PE=-m2+4m,由△PCE∽△DOA,可得$\frac{PC}{DO}$=$\frac{PE}{AD}$,构建二次函数后即可解决问题.
(3)①如图2中,取点F(1,4),连接AF、FB,首先证明△FAB是等腰直角三角形,推出∠FAB=45°,设直线AF交抛物线于P,可得直线AF的解析式为y=3x+1,利用方程组求出∠PAB=45°时,点P的坐标即可解决问题,再根据对称性求出P′A⊥PA时的点P′的坐标即可解决问题.
②观察图象可知点P的纵坐标的范围3<yp≤$\frac{97}{16}$或-$\frac{11}{18}$≤yP<3
,所以整数yp为4,5,6,0,1,2,又点P的横坐标$\frac{3}{2}$≤m<4.推出对应的点P有7个,
解答 解:(1)由题意A(0,1),B(4,3),
把A(0,1),B(4,3)代入y=-x2+bx+c得到$\left\{\begin{array}{l}{c=1}\\{-16+4b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=\frac{9}{2}}\\{c=1}\end{array}\right.$,
∴抛物线的解析式为y=-x2+$\frac{9}{2}$x+1.
(2)作PF⊥x轴于F,交AB于E,直线AB交x轴于D.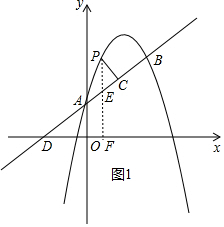
由题意D(-2,0),A(0,1),
设P(m,-m2+$\frac{9}{2}$m+1),则E(m,$\frac{1}{2}$m+1),PE=-m2+4m
∴OA=1,OD=2,AD=$\sqrt{5}$,
∵PF∥OA,
∴∠DAO=∠DEF=∠PEC,
∵∠AOD=∠PCE=90°,
∴△PCE∽△DOA,
∴$\frac{PC}{DO}$=$\frac{PE}{AD}$,
∴$\frac{PC}{2}$=$\frac{-{m}^{2}+4m}{\sqrt{5}}$,
∴PC=-$\frac{2\sqrt{5}}{5}$(m2-4m),
∵PC=-$\frac{2\sqrt{5}}{5}$(m2-4m)=-$\frac{2\sqrt{5}}{5}$(m-2)2+$\frac{8\sqrt{5}}{5}$,
∵-$\frac{2\sqrt{5}}{5}$<0,
∴m=2时,PC有最大值.最大值为$\frac{8\sqrt{5}}{5}$,此时P(2,6);
(3)①如图2中,取点F(1,4),连接AF、FB,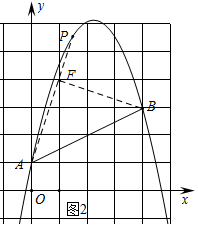
∵A(0,1),B(4,3),
∴AF=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,FB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴AF=FB,AF2+BF2=AB2,
∴△FAB是等腰直角三角形,
∴∠FAB=45°,设直线AF交抛物线于P,
∴直线AF的解析式为y=3x+1,
由$\left\{\begin{array}{l}{y=-{x}^{2}+\frac{9}{2}x+1}\\{y=3x+1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{11}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$,
∵A(0,1),
∴P($\frac{3}{2}$,$\frac{11}{2}$),
当P′A⊥PA时,
直线P′A的解析式为y=-$\frac{1}{3}$+1,
$\left\{\begin{array}{l}{y=-\frac{1}{3}x+1}\\{y=-{x}^{2}+\frac{9}{2}x+1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{29}{6}}\\{y=-\frac{11}{18}}\end{array}\right.$,
∴P′($\frac{29}{6}$,-$\frac{11}{18}$)
∴观察图象可知,满足条件0°<∠PAB≤45°的点P的横坐标$\frac{3}{2}$≤m<4或4<m≤$\frac{29}{6}$.
②观察图象可知点P的纵坐标的范围3<yp≤$\frac{97}{16}$或-$\frac{11}{18}$≤yP<3
∴整数yp为4,5,6,0,1,2,又点P的横坐标$\frac{3}{2}$≤m<4或4<m≤$\frac{29}{6}$.
∴对应的点P有7个,对应的点P的纵坐标为0,1,2,4,5,6,6,
∴“巧点”的个数为7个.
点评 本题考查二次函数的性质、一次函数的性质、相似三角形的判定和性质、等腰直角三角形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,学会添加辅助线,构造特殊三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
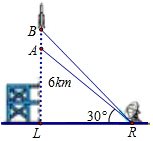 如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.
如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.| A. | 3$\sqrt{3}$-3 | B. | 3$\sqrt{3}$ | C. | 3$\sqrt{3}$+3 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com