
分析 先求出正三角形的外接圆的半径,再求出正三角形的边长,最后求其面积即可.
解答 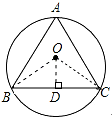 解:如图所示,
解:如图所示,
连接OB、OC,过O作OD⊥BC于D,
∵⊙O的面积为2π
∴⊙O的半径为$\sqrt{2}$
∵△ABC为正三角形,
∴∠BOC=$\frac{360°}{3}$=120°,∠BOD=$\frac{1}{2}$∠BOC=60°,OB=$\sqrt{2}$,
∴BD=OB•sin∠BOD=$\sqrt{2}$=$\frac{\sqrt{6}}{2}$,
∴BC=2BD=$\sqrt{6}$,
∴OD=OB•cos∠BOD=$\sqrt{2}$•cos60°=$\frac{\sqrt{2}}{2}$,
∴△BOC的面积=$\frac{1}{2}$•BC•OD=$\frac{1}{2}$×$\sqrt{6}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{3}}{2}$,
∴△ABC的面积=3S△BOC=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
故答案为:$\frac{{3\sqrt{3}}}{2}$.
点评 本题考查的是三角形的外接圆与外心,根据题意画出图形,利用数形结合求解是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
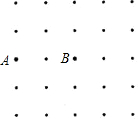 如图,由25个点构成的5×5的正方形点阵中,横纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以A,B为顶点,面积为2的阵点平行四边形的个数为9个.
如图,由25个点构成的5×5的正方形点阵中,横纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以A,B为顶点,面积为2的阵点平行四边形的个数为9个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 226.3×104 | B. | 2.263×105 | C. | 2.263×106 | D. | 2.263×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②③④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com