
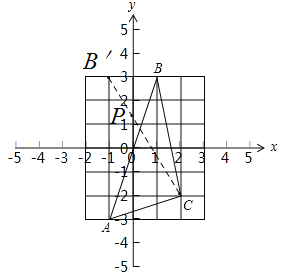
【题目】如图,图中的小方格都是边长为1的正方形,若点A(x,![]() ),点B(2x1,
),点B(2x1,![]() ),点C(z+1,
),点C(z+1,![]() ),已知点A,B关于原点对称,点C在二,四象限平分线上.
),已知点A,B关于原点对称,点C在二,四象限平分线上.
(1)求A、B、C点的坐标;
(2)结合A、B、C的坐标,在图中建立平面直角坐标系;
(3)在(2)的条件下,若P为y轴上的一个动点,请直接写出使△PBC周长最小的点P的坐标.
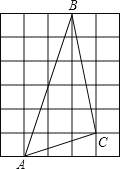
【答案】见解析
【解析】
(1)由于点A、B关于原点对称,所以它们的横坐标互为相反数,纵坐标也互为相反数,列方程组分别求出x、y的值即可求出点A、B的坐标,由点C在二、四象限的角平分线上可得点C的横纵坐标互为相反数,列方程求出z的值即可求出点C的坐标;(2)结合A、B、C三点的坐标建立直角坐标系即可;(3)要使△PBC周长最短,即要使PB与PC的和最小,作点B关于y轴的对称点点B',连接C B'与y轴交于点P,此时△PBC的周长最小,求出点P的坐标即可.
(1)由题意得: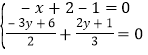 ,解得
,解得![]() ,
,
∴A(﹣1,﹣3),B(1,3),
由题意得:z+1+![]() =0,解得z=1,
=0,解得z=1,
∴C(2,﹣2);
(2)如右图所示:
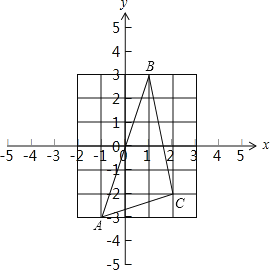
(3)作点B关于y轴的对称点点B',连接C B'与y轴交于点P,此时△PBC的周长最小,
∴B'(﹣1,3),
设直线B'C的解析式为y=kx+b,
![]() ,
,
∴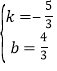 ,
,
∴y=﹣![]() x+
x+![]() ,
,
令x=0,y=![]() .
.
∴P(0,![]() ).
).
∴


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,∠ABC=120°,将△ABC绕点B逆时针旋转α,其中0°<α<90°得△A1BC1 , A1B交AC与点E,A1C1分别交AC、BC于D、F两点. 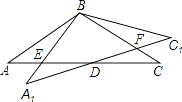
(1)在旋转过程中,线段EA1与FC有怎样的数量关系?证明你的结论;
(2)当α=30°时,试判断四边形BC1DA的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为4,边
的边长为4,边![]() 在
在![]() 轴上,边
轴上,边![]() 在
在![]() 轴上,点
轴上,点![]() 是
是![]() 轴上一点,坐标为
轴上一点,坐标为![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1)点![]() 的坐标为;
的坐标为;
(2)判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点P0的坐标为(![]() ,
,![]() ),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )
),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )

A. (![]() ,
,![]() ) B. (0,22018) C. (
) B. (0,22018) C. (![]() ,
,![]() ) D. (22018,0)
) D. (22018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知将![]() 沿
沿![]() 所在直线翻折,点
所在直线翻折,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合,对折边
重合,对折边![]() ,折痕也经过点
,折痕也经过点![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
⑤若![]() ,则
,则![]() 是等边三角形.
是等边三角形.
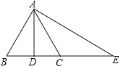
A. 只有①②正确 B. ①②③
C. ①②③④ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,点P为BC边上一动点,连接AP,将线段AP绕P点顺时针旋转90°,点A恰好落在直线CD上点E处.
(1)如图1,点E在线段CD上,求证:AD+DE=2AB;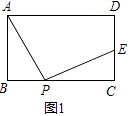
(2)如图2,点E在线段CD的延长线上,且点D为线段CE的中点,在线段BD上取点F,连接AF、PF,若AF=AB.求证:∠APF=∠ADB.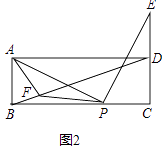
(3)如图3,点E在线段CD上,连接BD,若AB=2,BD∥PE,则DE= . (直接写出结果)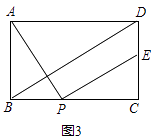
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG. 
(1)求证:∠EFG=∠B;
(2)若AC=2BC=4 ![]() ,D为AE的中点,求FG的长.
,D为AE的中点,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,则水的最大深度CD为( ) 
A.4cm
B.3cm
C.2cm
D.1cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com