
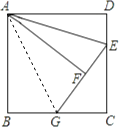
【题目】如图,正方形ABCD中,E为CD上一点,以AE为对称轴将△ADE翻折得到△AFE,延长EF交BC于G,若BG=CG,则sin∠EGC= . 
【答案】![]()
【解析】解:连接AG,
∵将△ADE翻折得到△AFE,
∴AB=AD=AF,AG=AG,∠D=∠B=∠AFG=90°,
在Rt△ABG与Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),
BG=FG,
设CG为x,则GF=BG=x,
在Rt△EGC中,CG2+EC2=EG2,
即x2+CE2=(3x﹣CE)2,
解得,CE= ![]() x,
x,
∴EG= ![]() x,
x,
∴sin∠EGC= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握正方形的性质和翻折变换(折叠问题)是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】白色污染( Whitepollution)是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓.为了让全校同学感受丢弃塑料袋对环境的影响,小彬随机抽取某小区![]() 户居民,记录了这些家庭
户居民,记录了这些家庭![]() 年某个月丢弃塑料袋的数量(单位:个)
年某个月丢弃塑料袋的数量(单位:个)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请根据上述数据,解答以下问题:

(1)小彬按“组距为![]() ”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
分组 | 划记 | 频数 |
| _______ | ________ |
|
|
|
| _______ | ________ |
|
|
|
合计 | / |
|
(2)根据(1)中的直方图可以看出,这![]() 户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,小彬又画出了如图所示的扇形统计图.请将统计图中各组占总数的百分比填在图中,并求出![]() 组对应的扇形圆心角的度数;
组对应的扇形圆心角的度数;
(4)若该小区共有![]() 户居民家庭,请你估计每月丢弃的塑料袋数量不小于
户居民家庭,请你估计每月丢弃的塑料袋数量不小于![]() 个的家庭个数.
个的家庭个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5)B. (5,2)C. (2,﹣5)D. (5,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 , x2 , 且x12+x22=10,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在AB边上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)若△ABC的底边长5,周长为21,求△BCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连BD.
(1)在图1中,求证:DB=DI;
(2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《重庆市生活垃圾分类管理办法》于2019年开始实施我校为积极响应政府对垃圾分类处理的号召,开展了垃圾分类网上知识竞赛,并从该校七年级随机抽取了部分学生的竞赛成绩进行整理、描述和分析(根据成绩共分![]() 四个等级),其中获得
四个等级),其中获得![]() 等级和
等级和![]() 等级的人数相等.
等级的人数相等.
下面给出了相应的条形统计图和扇形统计图:

根据以上信息,解答下列问题:
(1)共抽取了______名学生;
(2)补全条形统计图,并求出扇形统计图中![]() 等级对应的圆心角的度数;
等级对应的圆心角的度数;
(3)A等级中有![]() 名同学是女生,学校计划从
名同学是女生,学校计划从![]() 等级的学生中抽取
等级的学生中抽取![]() 名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少?
名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com