
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC��б��AB��x���ϣ�AB=25������C��y��ĸ������ϣ�AO:OC=3:4,��P���߶�OC�ϣ���PO��PC�ij�(PO<PC)�ǹ���x�ķ���x2-12x+32=O��������
(1) ��P��������
(2) ��AC��BC�ij���
(3)��x�����Ƿ���ڵ�Q��ʹ�Ե�A��C��P��QΪ������ı���������?�����ڣ���ֱ��д��ֱ��PQ�Ľ���ʽ���������ڣ���˵�����ɣ�

���𰸡���1��P��0����4�� ��2��AC=15 BC=20 ��3��y=��![]() ��4��y=��
��4��y=��![]() ��4
��4
�������������������1�����ݷ��̵Ľ����������Ȼ���PO��PC�����P�����ꣻ��2������˫��ֱ�ó���ACO=��ABC��Ȼ�������ABC������ֵ���AC��BC�ij��ȣ���3�����ݵ������ε����������Q�����꣬Ȼ�����PQ�ĺ�������ʽ.
�����������1��![]() -12x+32=O�����
-12x+32=O�����![]() =4��
=4��![]() =8 �� PO<PC��
=8 �� PO<PC��
�� PO=4�� �� P��O��-4��
��2���� ��ACB=90����CO��AB�� �� ��ACO=��ABC�� �� tan��ABC=![]() ��
��
Rt��ABC����AC=3a��BC=4a ��AB=5a��
��AB=5a=25 �� a=5 �� AC="15" BC=20
��3�����ڣ�ֱ��PQ����ʽΪ��y=��![]() ��4��y=��
��4��y=��![]() ��4.
��4.


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ϸ�Ĺ۲�ͼ�����������ʽ��Ȼ�������⣺ �� ![]() ��2+1=2��S1=
��2+1=2��S1= ![]()
�� ![]() ��2+1=3��S2=
��2+1=3��S2= ![]()
�� ![]() ��2+1=4��S3=
��2+1=4��S3= ![]()

��1���ú�n��n�����������ĵ�ʽ��ʾ�����仯���ɣ�
��2������S12+S22+S32+S42+��+S102��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD�У�PΪ�Խ���BD�ϵ�һ�㣬��E��AD���ӳ����ϣ���PA=PE��PE��CD��F������CE��
��1����֤����PCE�ǵ���ֱ�������Σ�
��2����ͼ2����������ABCD��Ϊ����ABCD�������������䣬����ABC=120��ʱ���жϡ�PCE����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�θ��ִ����У�10λ��ί��ij���ִ�ֱַ�Ϊ��9.8��9.0��9.5��9.7��9.6��9.0��9.0��9.5��9.9��8.9����ȥ��һ����߷�һ����ͷֺø��ֵĵ÷�Ӧ��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����A=30�㣬EΪBC�ӳ�����һ�㣬��ABC���ACE��ƽ�����ཻ�ڵ�D�����D�Ķ���Ϊ�� �� 
A.15��
B.17.5��
C.20��
D.22.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���̵����װ�ޣ�����ס�������װ����ͬʱʩ����8�������ɣ��踶��������ù�3520Ԫ����������鵥����6�죬�������鵥����12�������ɣ��踶��������ù�3480Ԫ���ʣ�
��1���ס������鵥������һ�죬�̵�Ӧ��������Ԫ��
��2����֪���鵥�������Ҫ12�죬���鵥�������Ҫ24�죬���������飬�̵�Ӧ�����ý��٣�
��3����װ������̵�ÿ���ӯ��200Ԫ������Ϊ��ΰ���ʩ���������̵꾭Ӫ��˵˵�������.������ֱ���ã�1����2���е���֪������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ĸ���˿����������������ľ��Χ��һ��ľ����״���ޣ���������˿��С��������������˿�ľ�������Ϊ3��4��5��7����������ľ���ļнǾ��ɵ�����������ľ���ļн�ʱ���ƻ���ľ��������������˿��ľ�������ֵΪ��������
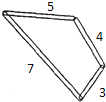
A. 6 B. 7 C. 8 D. 9
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com