
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转40°得到△A1BC1,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.

求证:ΔBCF≌ΔBA1D.
当∠C=40°时,请你证明四边形A1BCE是菱形.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)根据旋转的性质,得出A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,再根据ASA即可判定△BCF≌△BA1D;
(2)根据∠C=40°,△ABC是等腰三角形,即可得出∠A=∠C1=∠C=40°,进而得到∠C1=∠CBF,∠A=∠A1BD,由此可判定A1E∥BC,A1B∥CE,进而得到四边形A1BCE是平行四边形,最后根据A1B=BC,即可判定四边形A1BCE是菱形.
(1)∵△ABC是等腰三角形,
∴AB=BC,∠A=∠C,
∵将等腰△ABC绕顶点B逆时针方向旋转40度到△A1BC1的位置,
∴A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,
在△BCF与△BA1D中,  ,
,
∴△BCF≌△BA1D(ASA);
(2)∵∠C=40°,△ABC是等腰三角形,
∴∠A=∠C1=∠C=40°,
∴∠C1=∠CBF=40°,∠A=∠A1BD=40°,
∴A1E∥BC,A1B∥CE,
∴四边形A1BCE是平行四边形,
∵A1B=BC,
∴四边形A1BCE是菱形.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
档次 | 工资(元) | 频数(人) | 频率 |
A | 3000 | 20 | |
B | 2800 | 0.30 | |
C | 2200 | ||
D | 2000 | 10 |
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2![]() ,求阴影部分的面积.
,求阴影部分的面积.
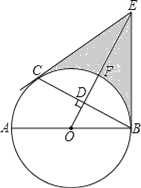
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现:
任意三个连续偶数的平方和是![]() 的倍数.
的倍数.
验证:
(1)![]() 的结果是
的结果是![]() 的几倍?
的几倍?
(2)设三个连续偶数的中间一个为![]() ,写出它们的平方和,并说明是
,写出它们的平方和,并说明是![]() 的倍数.
的倍数.
延伸:
(3)任意三个连续奇数的平方和,设中间一个为![]() ,被
,被![]() 整除余数是几呢?请写出理由.
整除余数是几呢?请写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC平分∠MON,P为OC上一点,PA⊥OM,PB⊥ON,垂足分别为A、B,连接AB,得到以下结论:(1)PA=PB;(2)OA=OB;(3)OP与AB互相垂直平分;(4)OP平分∠APB,正确的个数是( )
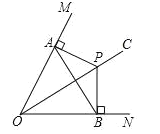
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y= ![]() 2+b
2+b![]() +c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)若M是抛物线的对称轴与直线BC的交点,N是抛物线的顶点,求MN的长;
(3)设点P是(1)中的抛物线的一个动点,是否存在满足S△PAB=8的点P?如存在请求出P的坐标;若不存在,请说明理由.


图1 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区举行“互联网+”征文比赛,已知每篇参赛征文成绩记![]() 分
分![]() ,组委会从
,组委会从![]() 篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表:
篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表:
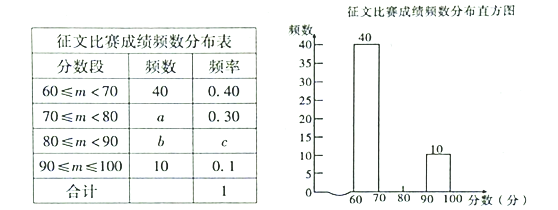
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中![]() 的值是 ;
的值是 ;
(2)请求出![]() 的值,再补全征文比赛成绩频数分布直方图;
的值,再补全征文比赛成绩频数分布直方图;
(3)若绘制扇形统计图,分别计算分数段![]() ,所对应扇形的圆心角度数.
,所对应扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(一)知识链接
若点M,N在数轴上,且M,N代表的实数分别是a,b,则线段MN的长度可表示为 .
(二)解决问题
如图,将一个三角板放置在平面直角坐标系中,∠ACB=90°,AC=BC,点B,C的坐标分别为(-2,-4),(-4,0).
(1)求点A的坐标及直线AB的表达式;
(2)若P是x轴上一点,且S△ABP=6,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:对角线互相平分的四边形是平行四边形.
小明同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程:
已知:如图,在四边形ABCD中,AC、BD相交于点O, .
求证: .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com