分析:作出图形,连接OP,根据轴对称的性质可得OP1=OP=OP2,∠BOP=∠BOP1,∠AOP=∠AOP2,然后求出∠P1OP2=2∠AOB=60°,再根据有一个角是60°的等腰三角形是等边三角形判定.
解答: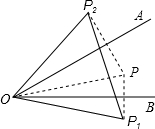
解:如图,连接OP,
∵P
1与P关于OB对称,P
2与P关于OA对称,
∴OP
1=OP,OP=OP
2,∠BOP=∠BOP
1,∠AOP=∠AOP
2,
∴OP
1=OP
2,
∠P
1OP
2=∠BOP+∠BOP
1+∠AOP+∠AOP
2=2∠BOP+2∠AOP=2∠AOB,
∵∠AOB=30°,
∴∠P
1OP
2=60°,
∴△P
1OP
2是等边三角形.
故答案为:等边.
点评:本题考查了轴对称的性质,等边三角形的判定,熟练掌握轴对称的性质求出△P1OP2的两边相等且有一个角是60°是解题的关键,作出图形更形象直观.

 解:如图,连接OP,
解:如图,连接OP,
