
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
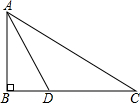 如图所示,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果精确到0.1)
如图所示,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
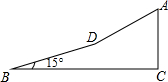 如图,某校八年级(1)班学生利用寒假期间到郊区进行社会实践活动,活动之余,同学们准备攀登附近的一个小山坡,从B点出发,沿坡脚15°的坡面以5千米/时的速度行至D点,用了10分钟,然后沿坡比为1:$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点,用了5分钟,求小山坡的高(即AC的长度)(精确到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732)
如图,某校八年级(1)班学生利用寒假期间到郊区进行社会实践活动,活动之余,同学们准备攀登附近的一个小山坡,从B点出发,沿坡脚15°的坡面以5千米/时的速度行至D点,用了10分钟,然后沿坡比为1:$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点,用了5分钟,求小山坡的高(即AC的长度)(精确到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
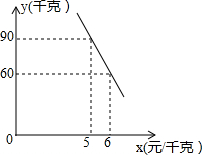 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.| 蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
| 所付的金额(元) | … | 125 | 300 | 300 | 360 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:用一段长为30m的篱笆围成一边靠墙的矩形菜园,墙长为18m,设菜园的宽AB为xm,面积为Sm2.
如图:用一段长为30m的篱笆围成一边靠墙的矩形菜园,墙长为18m,设菜园的宽AB为xm,面积为Sm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com