
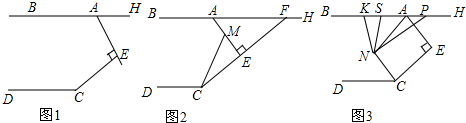
分析 (1)延长AE交DC于F,根据AE⊥CE垂直可得∠CEF=90°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠DCE-∠AFD=∠CEF=90°,从而得到∠HAE=∠AFD,再根据内错角相等,两直线平行即可得证;
(2)延长AE交DC的延长线于点G,由(1)得,BH∥CD,∠FAE=∠CGE,根据AE⊥CE可知∠CEG=90°,由三角形外角的性质得出∠DCM+∠MCE=∠CGE+90°,即∠DCM+∠MCE=∠FAE+90°,再根据∠MCE=∠AFC=90°-∠FAE即可得出结论;
(3)延长CE交BA的延长线于点Q,延长PN交CD的延长线为M,根据,∠BAN:∠EAN=∠DCN:∠ECN=1:2,∠DCE-∠HAE=90°及平角定义,可得出∠BAN+∠DCN=90°,根据平行线的性质、三角形外角的性质,可得到∠APN+∠DCN=∠PNC=2∠ANS+∠ANP,③根据∠BAN=∠ANP+∠APN,∠BAN+∠DCN=90°,可得出∠ANP+∠APN+∠DCN=90°④,利用③+④,可推得∠APN+∠DCN=∠ANS+45°的关系,即得出结论.
解答  (1)证明:如图,延长AE交DC于F,
(1)证明:如图,延长AE交DC于F,
∵AE⊥CE,
∴∠CEF=90°,
根据三角形的外角性质,∠DCE-∠AFD=∠CEF=90°,
又∵∠DCE-∠HAE=90°,
∴∠HAE=∠AFD,
∴BH∥CD;
(2)证明:延长AE交DC的延长线于点G,
∵由(1)得,BH∥CD,
∴∠FAE=∠CGE.
∵AE⊥CE,
∴∠AEF=∠CEG=90°,
∴∠AFC=90°-∠FAE.
∵∠DCE是△CEG的外角,
∴∠DCM+∠MCE=∠CGE+90°,即∠DCM+∠MCE=∠FAE+90°,
∴∠MCE=∠AFC=90°-∠FAE,
∴∠DCM+90°-∠FAE=∠FAE+90°,即∠MCD=2∠FAE;
(3)证明:延长CE交BA的延长线于点Q,延长PN交CD的延长线为M,
∵∠BAN:∠EAN=1:2,
∴∠5+2∠5+∠1=180° ①
∵∠DCN:∠ECN=1:2,∠DCE-∠HAE=90°,
∴∠2+2∠2-∠1=90° ②
由①+②,得 3∠5+3∠2=270°,
∴∠5+∠2=90°
∵AB∥CD,
∴∠APN=∠NMC,
又∵∠NMC+∠2=∠6,
∴∠APN+∠2=∠6
∵NP平分∠KNC,NS平分∠KMA,
∴∠KNA=2∠4,∠6=2∠4+∠3,
∴∠APN+∠2=2∠4+∠3 ③
∵∠5=∠3+∠APN,∠5+∠2=90°,
∴∠3+∠APN+∠2=90° ④
③+④,化简得:∠APN+∠2=∠4+45°,
∴∠APN+∠2-∠4=45°,即:∠DCN+∠APN-∠ANS=45°.
点评 本题主要考查了平行线的性质及判断、平行线的性质、三角形外角的性质等知识,添加合适的辅助线是解决此题的关键.对于第(3)小题,理清各角之间的联系是重中之重.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
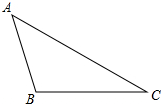 (1)如图,过顶点B的一条直线把△ABC分割成两个等腰三角形,当∠C是其中一个等腰三角形的顶角,∠C=40°时,∠ABC=105度;当∠C为△ABC中最小时,探究∠ABC与∠C之间的数量关系;
(1)如图,过顶点B的一条直线把△ABC分割成两个等腰三角形,当∠C是其中一个等腰三角形的顶角,∠C=40°时,∠ABC=105度;当∠C为△ABC中最小时,探究∠ABC与∠C之间的数量关系;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com