
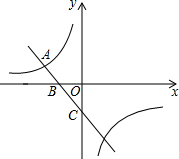
 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a).
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a).分析 (1)将x=-2代入一次函数解析式中求出a的值,根据点A的坐标利用反比例函数图象上点的坐标特征即可求出k值,从而得出结论;
(2)联立一次函数与反比例函数解析式成方程组,解方程组求出两函数图象除点A外的另一点坐标,结合函数图象的上下位置关系以及两交点的横坐标即可得出不等式的解集;
(3)根据一次函数的解析式求出点B、C的坐标,设点P的坐标为(m,-$\frac{2}{m}$),根据三角形的面积公式结合S△BOP=4S△OBC,即可得出关于m的方程,解方程即可得出m的值,再将其代入点P的坐标即可得出结论.
解答 解:(1)∵点A(-2,a)在一次函数y=-x-1的图象上,
∴a=-1×(-2)-1=1,
∴点A(-2,1).
∵点A(-2,1)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=-2×1=-2,
∴反比例函数的表达式为y=-$\frac{2}{x}$.
(2)联立一次函数与反比例函数解析式得:$\left\{\begin{array}{l}{y=-x-1}\\{y=-\frac{2}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,
∴反比例函数与一次函数图象的另一个交点为(1,-2).
观察函数图象可知:
当-2<x<0或x>1时,反比例函数图象在一次函数图象的上方,
∴不等式$\frac{k}{x}$>-x-1的解集为-2<x<0或x>1.
(3)令y=-x-1中x=0,则y=-1,
∴点C(0,-1);
令y=-x-1中x=0,则-x-1=0,解得:x=-1,
∴点B(-1,0).
设点P的坐标为(m,-$\frac{2}{m}$),
∵S△BOP=4S△OBC,
∴$\frac{1}{2}$BO•|yP|=4×$\frac{1}{2}$OB•OC,即|-$\frac{2}{m}$|=4,
解得:m=±$\frac{1}{2}$,
∴点P的坐标为($\frac{1}{2}$,-4)或(-$\frac{1}{2}$,4).
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及三角形的面积公式,解题的关键是:(1)求出点A的坐标;(2)求出两函数图象除点A外另一交点的坐标;(3)得出关于点P纵坐标的方程.本题属于中档题,难度不大,解决该题型题目时,联立两函数解析式求出交点坐标是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (2,9) | B. | (5,2) | C. | (1,-5) | D. | (-9,-5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF.在不添加辅助线的情况下,请写出与∠AEF相等的所有角∠DCF,∠BCF,∠DFC.
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF.在不添加辅助线的情况下,请写出与∠AEF相等的所有角∠DCF,∠BCF,∠DFC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
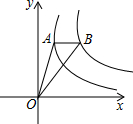 如图,点A是反比例函数y1=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{k}{x}$(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为5.
如图,点A是反比例函数y1=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{k}{x}$(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com