
【题目】如图,已知CD是AB的中垂线,垂足为D,DE⊥AC于点E,DF⊥BC于点F.

(1)求证:DE=DF;
(2)若线段CE的长为3 cm,BC的长为4 cm,求BF的长.
科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a= , b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为D的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,Rt△ABC中,∠ACB=90°,D为AB中点,DE、DF分别交AC于E,交BC于F,且DE⊥DF.
(1)如果CA=CB,求证:AE2+BF2=EF2;
(2)如图2,如果CA<CB,(1)中结论还能成立吗?若成立,请证明;若不成立,请说明理由.
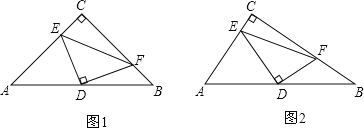
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC=6,分别以点A和点C为圆心,以相同的长(大于 ![]() AC)为半径作弧,两弧相交于点M和点N , 作直线MN交AB于点D , 交AC于点E , 连接CD . 则DE的长为 .
AC)为半径作弧,两弧相交于点M和点N , 作直线MN交AB于点D , 交AC于点E , 连接CD . 则DE的长为 . 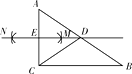
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线经过点A(-2,0)、B(4,0)、C(0,-8),抛物线y=ax2+bx+c(a≠0)与直线y=x-4交于B , D两点.
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为抛物线上的一个动点,且在直线BD下方,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F , 交抛物线于点G . 当△QDG为直角三角形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: 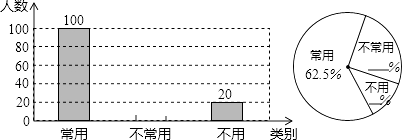
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com