
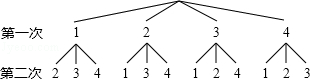
| 第一次 第二次 | 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | ① | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
分析 (1)第1次抽到1,而第二次没有抽到1,则可判断小明的游戏规则为:随机抽出一张卡片后不放回,再随机抽出一张卡片;
(2)利用第一次抽到3,第2次抽到2写出有序实数对;
(3)根据概率公式分别计算出两种游戏规则下的两次抽到的数字之和为奇数的概率,然后通过比较概率的大小判断谁获胜的可能性大.
解答 解:(1)小明的游戏规则为:随机抽出一张卡片后不放回,再随机抽出一张卡片实数;
(2)根据小华的游戏规则,表格中①表示的有序数对为(3,2);.
故答案为不放回,(3,2);
(3)小明获胜的可能性大.理由如下:
由树状图得,共有12种等可能的结果,其中数字之和为奇数的有8种,所以两次抽到的数字之和为奇数的概率=$\frac{8}{12}$=$\frac{2}{3}$:
由列表得,共有16种等可能的结果,其中数字之和为奇数的有8种,所以两次抽到的数字之和为奇数的概率=$\frac{8}{16}$=$\frac{1}{2}$,
∵$\frac{2}{3}$>$\frac{1}{2}$,
∴小明获胜的可能性大.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
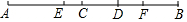 如图,C、D是线段AB上的点,E为AD中点,F为BC中点.
如图,C、D是线段AB上的点,E为AD中点,F为BC中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
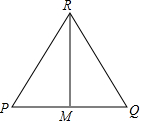 已知:如图,△RPQ中,RP=RQ,M为PQ的中点.
已知:如图,△RPQ中,RP=RQ,M为PQ的中点.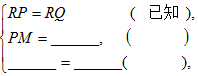
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com