
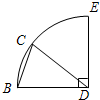
 如图,弧BE是⊙D的$\frac{1}{4}$圆周,点C在弧BE上运动(不与B重合),则∠C的取值范围是( )
如图,弧BE是⊙D的$\frac{1}{4}$圆周,点C在弧BE上运动(不与B重合),则∠C的取值范围是( )| A. | 0°≤∠C≤45° | B. | 0°<∠C≤45° | C. | 45°<∠C<90° | D. | 45°≤∠C<90° |
分析 由于$\widehat{BE}$是⊙D的$\frac{1}{4}$圆周,则可计算出∠BDE=90°,再根据等腰三角形的性质由DB=DC,则∠B=∠BCD,于是根据三角形内角和定理得到∠BCD=90°-$\frac{1}{2}$∠BDC,然后根据0≤∠BDC≤90°求∠BCD的取值范围.
解答 解:∵$\widehat{BE}$是⊙D的$\frac{1}{4}$圆周,
∴∠BDE=$\frac{1}{4}$×360°=90°,
∵DB=DC,
∴∠B=∠C,
∴∠C=$\frac{1}{2}$(180°-∠BDC)=90°-$\frac{1}{2}$∠BDC,
∵0≤∠BDC≤90°,
∴45°≤∠C≤90°,
故选D.
点评 本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com