Question

【题目】如图，已知二次函数y=ax2﹣（2a﹣）x+3的图象经过点A（4，0），与y轴交于点B．在x轴上有一动点C（m，0）（0＜m＜4），过点C作x轴的垂线交直线AB于点E，交该二次函数图象于点D．

（1）求a的值和直线AB的解析式；

（2）过点D作DF⊥AB于点F，设△ACE，△DEF的面积分别为S1，S2，若S1=4S2，求m的值；

（3）点H是该二次函数图象上位于第一象限的动点，点G是线段AB上的动点，当四边形DEGH是平行四边形，且DEGH周长取最大值时，求点G的坐标．

Answer 1

【答案】（1）y=﹣；（2）m值为；（3）点G坐标为（，）或（，）

【解析】

（1）把点A坐标代入y=ax2﹣（2a﹣）x+3可求a，用待定系数法求直线AB的解析即可；（2）用含有m的代数式表示DE、AC的长，易证△DEF∽△AEC，S1=4S2，得到DE与AE的数量关系可以构造方程，解方程即可求得m的值；

（3）如图，过点G做GM⊥DC于点M，用含有n的代数式表示GH，由平行四边形性质DE=GH，可得m，n之间数量关系，利用相似用GM表示EG，即可用含有m的代数式表示DEGH周长，利用函数性质求出周长最大时的m值，可得n值，进而求G点坐标．

（1）把点A（4，0）代入，得0=a42﹣（2a﹣）×4+3，

解得a=﹣，

∴函数解析式为：y=；

设直线AB解析式为y=kx+b，

把A（4，0），B（0，3）代入得，

解得；

∴直线AB解析式为：y=﹣；

（2）由已知，点D坐标为（m，﹣），点E坐标为（m，﹣），

∴AC=4﹣m，DE=（﹣）﹣（﹣）=﹣，

∵BC∥y轴，

∴，

∴AE=，

∵∠DFA=∠DCA=90°，∠FBD=∠CEA，

∴△DEF∽△AEC；

∵S1=4S2，

∴AE=2DE，

∴，

解得m1=，m2=4（舍去），

故m值为；

（3）如图，过点G做GM⊥DC于点M，

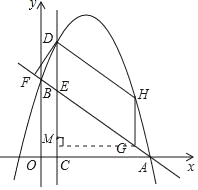
由（2）DE=﹣，同理HG=﹣；

∵四边形DEGH是平行四边形，

∴﹣=﹣，

整理得：（n﹣m）[]=0，

∵m≠n，

∴m+n=4，即n=4﹣m，

∴MG=n﹣m=4﹣2m

由已知△EMG∽△BOA，

∴，

∴EG=，

∴DEGH周长L=2[﹣+]=﹣，

∵a=﹣＜0，

∴m=﹣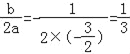时，L最大．

∴n=4﹣=，

∴G点坐标为（，），此时点E坐标为（，），

当点G、E位置对调时，依然满足条件，

∴点G坐标为（，）或（，）