Question

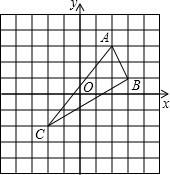
如图，已知△ABC．

(1)作出△ABC的内切圆I；

(2)设I与AC、AB、BC分别相切于点D、E、F，且AB＝5cm，BC＝9cm，AC＝6cm，求AE、BF和CD的长．

Answer 1

答案：
解析：

((1)作法　　作∠B，∠C的平分线，它们相交于I,过点I作IF⊥BC于F,以点I为圆心，IF长为半径作I，I就是所求的圆． 　　(2)　　由上面的作法可知：I是△ABC的内切圆，所以AD＝AE，BE＝BF，CD＝CF．设AD＝AE＝x cm，BE＝BF＝y cm，CD＝CF＝z cm，则有 　　 　　解得　　 　　所以AE、BF、CD的长分别是1cm、4cm、5cm． 　　评析：(1)由本题可知：任意一个三角形有且只有一个内切圆，(2)此题的解法体现了构造方程组来解决几何问题的思想方法，这种方法在今后解题中要能灵活运用．

提示：

思路与技巧：作圆的关键是确定圆心，由于所求的圆与△ABC的三边都相切，所以圆心到三边的距离相等，因此这个点既要在∠B的平分线上，又要在∠C的平分线上，显然这两条角平分线的交点就是圆心I，再根据切线长定理我们不难找出三个关系式，求出相关线段的长．