
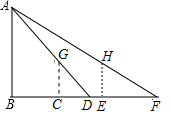
 小强为测量一路灯杆AB的高度,在灯光下,小强在C处的影长为3米,沿BC方向行走了5米到E处,此时小强的影长为5米,若小强身高为1.7米,求路灯杆AB的高度.
小强为测量一路灯杆AB的高度,在灯光下,小强在C处的影长为3米,沿BC方向行走了5米到E处,此时小强的影长为5米,若小强身高为1.7米,求路灯杆AB的高度. 分析 根据GC∥AB可得$\frac{GC}{AB}$=$\frac{DC}{DB}$,即$\frac{1.7}{AB}$=$\frac{3}{3+BC}$,再由HE∥AB可得$\frac{HE}{AB}$=$\frac{EF}{FB}$,即$\frac{1.7}{AB}$=$\frac{5}{10+BC}$,进而可得$\frac{3}{3+BC}=\frac{5}{10+BC}$,再解即可得到BC,进而可得AB的长.
解答 解:∵GC∥AB,
∴$\frac{GC}{AB}$=$\frac{DC}{DB}$,即$\frac{1.7}{AB}$=$\frac{3}{3+BC}$,
∵HE∥AB,
∴$\frac{HE}{AB}$=$\frac{EF}{FB}$,即$\frac{1.7}{AB}$=$\frac{5}{10+BC}$,
∴$\frac{3}{3+BC}=\frac{5}{10+BC}$,
∴BC=7.5,
∴AB=5.95,
∴灯杆AB的高度为5.95米.
点评 此题主要考查了相似三角形的应用,关键是掌握相似三角形的对应边的比相等.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
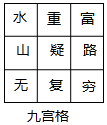 为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 70 | 80 | 90 |
| 男生(人) | 5 | 10 | 7 |
| 女生(人) | 4 | 13 | 4 |
| A. | 男生的平均成绩大于女生的平均成绩 | |
| B. | 男生的平均成绩小于女生的平均成绩 | |
| C. | 男生成绩的中位数大于女生成绩的中位数 | |
| D. | 男生成绩的中位数小于女生成绩的中位数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
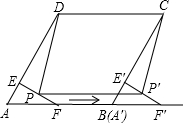 如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A'E'F'.设 P、P'分别是 EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )
如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A'E'F'.设 P、P'分别是 EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )| A. | 28$\sqrt{3}$ | B. | 24$\sqrt{3}$ | C. | 32$\sqrt{3}$ | D. | 32$\sqrt{3}$-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8岁 | B. | 9岁 | C. | 10岁 | D. | 11岁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com