
 如图,正方形ABCD中,点P为CD上一点,线段AP的垂直平分线MN交BD于点N,点M为垂足,交两边于点E、F,连接PN,则下列结论,其中正确的有( )
如图,正方形ABCD中,点P为CD上一点,线段AP的垂直平分线MN交BD于点N,点M为垂足,交两边于点E、F,连接PN,则下列结论,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①正确;过N作ST‖BC分别交AB、DC于S、T,则ST⊥AB,先证明△BSN是等腰直角三角形,得出SA=TN,再由AN=PN,证明Rt△ASN≌Rt△NTP,得出∠SAN=∠TNP,证出∠ANP=90°,得出∠PAN=45°,∠DAP=45°-∠SAN,再由∠DNT=∠BNS=45°,得出∠DNP=45°-∠TNP,即可得出∠DNP=∠DAP;
②正确;PC=PT+TC=SN+SB,△BSN是等腰直角三角形,SB=SN,即可得出PC=SN+SB=$\sqrt{2}$BN;
③正确;设正方形ABCD的边长为a,得出DP+DC=$\sqrt{2}$($\sqrt{2}$a-BN),DN=BD-BN═$\sqrt{2}$a-BN,即可得出结论;
④正确;过P作AD的平行线交MN于K,证出MF=MK,NE=NK,即可得出结论.
解答 解:①正确;过N作ST‖BC分别交AB、DC于S、T,如图所示: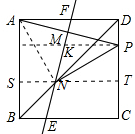 则ST⊥AB,
则ST⊥AB,
∵四边形ABCD是正方形,
∴AB=BC=ST,∠BAD=90°,∠ABD=45°,
∴△BSN是等腰直角三角形,
∴SB=SN,∠BNS=45°,
∴SA=TN,
∵线段AP的垂直平分线MN交BD于点N,
∴AN=PN,
在△RtASN和Rt△NTP中,
$\left\{\begin{array}{l}{AN=PN}&{\;}\\{SA=TN}&{\;}\end{array}\right.$,
∴Rt△ASN≌Rt△NTP(HL),
∴∠SAN=∠TNP,
∵∠SAN+∠ANS=90°,
∴∠TNP+∠ANS=90°,
∴∠ANP=90°,
∴∠PAN=45°,
∴∠SAN+∠DAP=45°,
∴∠DAP=45°-∠SAN,
∵∠DNT=∠BNS=45°,
∴∠DNP=∠DNT-∠PNT=45°-∠TNP,
∴∠DNP=∠DAP;
②正确;由①得:PC=PT+TC=SN+SB,△BSN是等腰直角三角形,SB=SN,
∴PC=SN+SB=$\sqrt{2}$BN;
③正确;设正方形ABCD的边长为a,
则DP+DC=2a-PC=2a-$\sqrt{2}$BN=$\sqrt{2}$($\sqrt{2}$a-BN),
DN=BD-BN═$\sqrt{2}$a-BN,
∴$\frac{DP+DC}{DN}$=$\frac{\sqrt{2}(\sqrt{2}a-BN)}{\sqrt{2}a-BN}$=$\sqrt{2}$;
④正确;过P作AD的平行线交MN于K,如图所示:
∵AM=PM,
∴MF=MK,
由①得:PT=SN=SB=CT,TN∥BC∥PK,
∴NE=NK,
∴MN=MF+NE;
综上所述:正确的结论有4个.
故选:D.
点评 本题考查了正方形的性质、全等三角形的判定与性质、线段垂直平分线的性质、等腰直角三角形的判定与性质;本题难度较大,综合性强,特别是需要通过作辅助线证明三角形全等、等腰直角三角形以及中点才能得出结论.


科目:初中数学 来源: 题型:解答题
 如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 3000 | 3050 | 3100 | 3150 | 3200 | 3250 | 3300 |
| y | 100 | 99 | 98 | 97 | 96 | 95 | 94 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3:2 | B. | 5:3 | C. | 8:5 | D. | 13:8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=4$\sqrt{3}$,∠DAB=90°,∠B=60°,AC⊥BC,
如图,在四边形ABCD中,AB=4$\sqrt{3}$,∠DAB=90°,∠B=60°,AC⊥BC,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com