
 x-3,并且与x轴、y轴分别相交于点A、B.
x-3,并且与x轴、y轴分别相交于点A、B.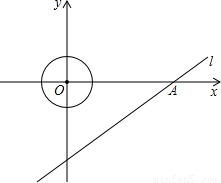
 x-3,并且与x轴、y轴分别相交于点A、B,所以分别令y=0;x=0,即可求出A、B的坐标;
x-3,并且与x轴、y轴分别相交于点A、B,所以分别令y=0;x=0,即可求出A、B的坐标;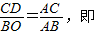
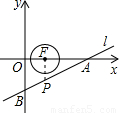
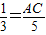 ,求出AC的值,即可得到此时OC的值,利用OC的长度结合速度即可求出时间;根据对称性,圆C还可能在直线l的右侧,与直线l相切,
,求出AC的值,即可得到此时OC的值,利用OC的长度结合速度即可求出时间;根据对称性,圆C还可能在直线l的右侧,与直线l相切,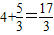 ,
,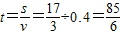 ;
;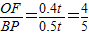 ,又
,又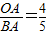 ,所以可得到
,所以可得到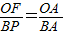 ,进而可得到FP∥OB,PF⊥OA,所以P点的横坐标为0.4t,又结合P点在直线AB上,可得P点的纵坐标为0.3t-3,因此可见:当PF=1时,P点在动圆上,当0≤PF<1时,P点在动圆内,而当P=1时,由对称性可知,有两种情况:①当P点在x轴下方时,PF=-(0.3t-3)=1,解之可得t的值,②当P点在x轴上方时,PF=0.3t-3=1,解之得t的另一个值,进而可得到当
,进而可得到FP∥OB,PF⊥OA,所以P点的横坐标为0.4t,又结合P点在直线AB上,可得P点的纵坐标为0.3t-3,因此可见:当PF=1时,P点在动圆上,当0≤PF<1时,P点在动圆内,而当P=1时,由对称性可知,有两种情况:①当P点在x轴下方时,PF=-(0.3t-3)=1,解之可得t的值,②当P点在x轴上方时,PF=0.3t-3=1,解之得t的另一个值,进而可得到当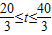 时,0≤PF≤1,并且此时点P在动圆的圆面上,所经过的时间为
时,0≤PF≤1,并且此时点P在动圆的圆面上,所经过的时间为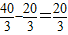 .
. x-3中,令x=0,得y=-3;令y=0,得x=4,故得A、B两的坐标为
x-3中,令x=0,得y=-3;令y=0,得x=4,故得A、B两的坐标为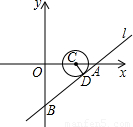
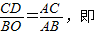
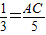 ,则AC=
,则AC= . (4分)
. (4分)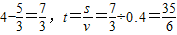 (秒). (5分)
(秒). (5分)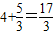 . (7分)
. (7分)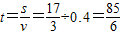 (秒).
(秒).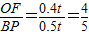 ,又
,又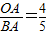 ,
,
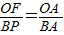 ,
,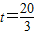 ;
;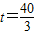 . (11分)
. (11分)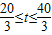 时,0≤PF≤1,此时点P在动圆的圆面上,所经过的时间为
时,0≤PF≤1,此时点P在动圆的圆面上,所经过的时间为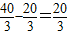 ,
,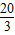 秒. (12分)
秒. (12分)

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
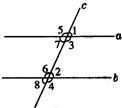 7、已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )
7、已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
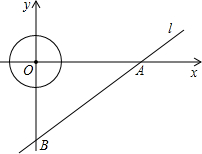 已知:如图所示,直线l的解析式为y=
已知:如图所示,直线l的解析式为y=| 3 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com