
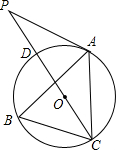
 ��ͼ����A��B��C�ֱ��ǡ�O�ϵĵ㣬�ҡ�B=60�㣬CD�ǡ�O��ֱ����P��CD�ӳ����ϵ�һ�㣬��AP=AC��
��ͼ����A��B��C�ֱ��ǡ�O�ϵĵ㣬�ҡ�B=60�㣬CD�ǡ�O��ֱ����P��CD�ӳ����ϵ�һ�㣬��AP=AC������ ��1����������OA���ɡ�B=60�㣬����Բ�ܽǶ�����������á�AOC�Ķ���������OA=OC��������á�OAC���OCA�Ķ�����������������ǵ����ʣ���á�AOP�Ķ���������AP=AC�����õȱ߶ԵȽǣ���á�P�������á�PAO=90�㣬���֤��AP�ǡ�O�����ߣ�
��2����AB��ֱ��ʱ���ı���ADBC�Ǿ��Σ��ڡ�ABC�ǵȱ�������ʱ����ABC��������
��� ��1��֤��������OA��
�ߡ�B=60�㣬
���AOC=2��B=120�㣬
�֡�OA=OC��
���ACP=��CAO=30�㣬
���AOP=60�㣬
��AP=AC��
���P=��ACP=30�㣬
���OAP=90�㣬
��OA��AP��
��AP�ǡ�O�����ߣ�
��2��������AD���ߡ�ADC=��B=60�㣬CD��ֱ����
���DAC=90�㣬��AC=3��
��AD=$\sqrt{3}$��CD=2$\sqrt{3}$��OC=$\sqrt{3}$��
��AB��ֱ��ʱ���ı���ADBC�Ǿ��Σ���ʱ$\widehat{BC}$=$\frac{60��•\sqrt{3}}{180}$=$\frac{\sqrt{3}}{3}$�У�
�ڡߡ�B=60�㣬
�൱BA=BCʱ����ABC��������ʱ��ABC�ǵȱ������Σ�
��$\widehat{BC}$=$\frac{120��•\sqrt{3}}{180}$=$\frac{2\sqrt{3}}{3}$�У�S��ABC=$\frac{\sqrt{3}}{4}$��32=$\frac{9\sqrt{3}}{4}$��
���� ���⿼�����ߵ��ж������ε��ж����ȱ������ε��ж������ʡ�������ʽ��֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ����������ѧ֪ʶ������⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬MN��C�㣬AD��MN��D��ACƽ�֡�DAB����֤��MNΪ��O�����ߣ�
��ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬MN��C�㣬AD��MN��D��ACƽ�֡�DAB����֤��MNΪ��O�����ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
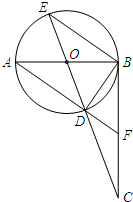 ��ͼ��AB�ǡ�O��ֱ����BC��AB������Ϊ��B������CO���ӳ�����O�ڵ�D��E������AD���ӳ���BC�ڵ�F�������н�����ȷ���У�������
��ͼ��AB�ǡ�O��ֱ����BC��AB������Ϊ��B������CO���ӳ�����O�ڵ�D��E������AD���ӳ���BC�ڵ�F�������н�����ȷ���У�������| A�� | �٢� | B�� | �ۢ� | C�� | �٢ڢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��0��b��0 | B�� | k��0��b��0 | C�� | k��0��b��0 | D�� | k��0��b��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
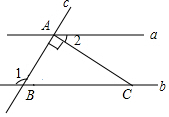 ��ͼ��ƽ��ֱ��a��b��ֱ��c���أ��ֱ��ཻ�ڵ�A��B������A��AC��AB����ֱ���ڵ�C������1=128�㣬���2�Ķ����ǣ�������
��ͼ��ƽ��ֱ��a��b��ֱ��c���أ��ֱ��ཻ�ڵ�A��B������A��AC��AB����ֱ���ڵ�C������1=128�㣬���2�Ķ����ǣ�������| A�� | 128�� | B�� | 90�� | C�� | 52�� | D�� | 38�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
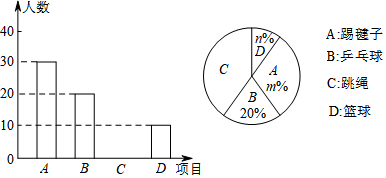
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com