练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．要使分式$\frac{x-3}{{{x^2}+6x+9}}$有意义，那么x的取值范围是（　　）
    A．x≠3B．x≠3且x≠-3C．x≠0且x≠-3D．x≠-3

    分析 根据分式有意义的条件列出关于x的不等式，求解即可．

    解答 解：∵x2+6x+9≠0，
    ∴（x+3）2≠0，
    ∴x+3≠0，
    ∴x≠-3，
    ∴分式$\frac{x-3}{{{x^2}+6x+9}}$有意义，x的取值范围x≠-3，
    故选D．

    点评 本题考查了分式有意义的条件：分母不为0，掌握不等式的解法是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．如图所示，长为2宽为1的矩形和边长为3的正方形在同一水平线上，矩形沿该水平线从左向右匀速穿过正方形；设穿过的时间为t，正方形除去矩形面积为S（阴影部分），则S与t的大致图象为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如图图形中，既是轴对称图形又是中心对称图形的是（　　）
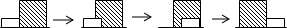
    A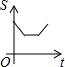．B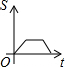．C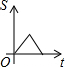．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．阅读对人成长的影响是巨大的，一本好书往往能改变人的一生，每年的4月23日被联合国教科文组织确定为“世界读书日”．某校本学年开展了读书活动，在这次活动中，八年级（1）班40名学生读书册数的情况如表：
    读书册数45678
    人数（人）6410128
    根据表中的数据，求：
    （1）该班学生读书册数的平均数；
    （2）该班学生读书册数的中位数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．在一个不透明的袋中装有一红一白2个球，这些球除颜色外都相同，小刚从袋中随机摸出一个球，记下颜色后放回袋中，再从袋中随机摸出一个球，两次都摸到红球的概率是$\frac{1}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列命题中，真命题的个数是（　　）
    ①同位角相等；
    ②a，b，c是三条直线，若a⊥b，b⊥c，则a⊥c．
    ③a，b，c是三条直线，若a∥b，b∥c，则a∥c；
    ④过一点有且只有一条直线与已知直线平行．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

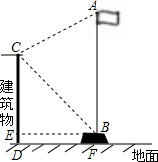    11．如图，张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°，旗杆底部B点的俯角为45°，若旗杆底部B点到该建筑物的水平距离BE=9米，旗杆台阶的高BF=0.6米，A、B、F在同一直线上，求旗杆顶部A离地面的高度AF（结果精确到0.1米，参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

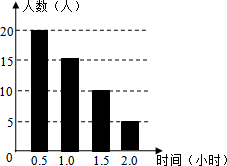    8．某校为了解学生课外阅读情况，随机调查了50名学生各自平均每天的课外阅读时间，并绘制成条形图，据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

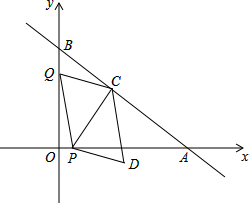    10．如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（8，0），B（0，6），动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点Q从点B出发，沿射线BO方向以每秒2个单位的速度运动，过点P作PC⊥AB于点C，连接PQ，CQ，以PQ，CQ为邻边构造?PQCD，设点P运动的时间为t秒．
    （1）当点Q在线段OB上时，用含t的代数式表示PC，AC的长；
    （2）在运动过程中，设△OPQ的面积为S．
    ①当点D落在x轴上时，求出满足条件的t的值；
    ②若点D落在△ABO内部（不包括边界）时，直接写出S的取值范围；
    （3）作点Q关于x轴的对称点Q′，连接CQ′，在运动过程中，是否存在某时刻使过A，P，C三点的圆与△CQQ′三边中的一条边相切？若存在，请求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案