
分析 (1)先变形为(4×5×3)×(106×107×105),再根据同底数幂的乘法法则计算即可求解;
(2)先算积的乘方,再计算单项式的乘法;
(3)根据单项式的乘法法则计算即可求解;
(4)先算积的乘方,再根据单项式的乘法法则计算即可求解;
(5)先算积的乘方,再计算单项式的乘法,注意整体思想的应用.
解答 解:(1)(4×106)×(5×107)×(3×105)
=(4×5×3)×(106×107×105)
=60×1018
=6×1019;
(2)$\frac{2}{3}$a3b2•(-$\frac{3}{2}$ab2)2;
=$\frac{2}{3}$a3b2•$\frac{9}{4}$a2b4
=$\frac{3}{2}$a5b6;
(3)3a2b3×(-$\frac{1}{6}$a3b4)×4abc2=-2a6b8c2;
(4)-2a3bc•(-ab2)•(-ab2)2;
=-2a3bc•(-ab2)•a2b4
=2a6b7c;
(5)$\frac{5}{8}$[(a+b)(a-b)]4•$\frac{4}{9}$(a+b)4(b-a)5
=$\frac{5}{8}$(a+b)4(a-b)4•$\frac{4}{9}$(a+b)4(b-a)5
=$\frac{5}{18}$(a+b)8(a-b)9.
点评 考查了整式的混合运算,熟练掌握积的乘方,同底数幂的乘法,单项式的乘法法则是解题的关键,注意整体思想的应用.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
 某五金厂生产的螺母形状如图所示
某五金厂生产的螺母形状如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,四边形ABCD中,AD⊥CD,BC⊥AB,AE平分∠BAD,CF平分∠DCB.AE交CD于点E,CF交AB于点F,问AE与CF是否平行?为什么?
已知,如图,四边形ABCD中,AD⊥CD,BC⊥AB,AE平分∠BAD,CF平分∠DCB.AE交CD于点E,CF交AB于点F,问AE与CF是否平行?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
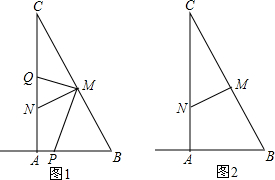
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com