

分析 (1)如图1中,连接OD,在Rt△ODC中,根据OD=$\sqrt{O{C}^{2}+C{D}^{2}}$计算即可.
(2)如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.在Rt△OCE中,根据OC=$\sqrt{O{E}^{2}+C{E}^{2}}$计算即可.
(3)如图3中,当OF⊥DE时,OF的值最大,设OF交DE于H,在OH上取一点M,使得OM=DM,连接DM.分别求出MH、OM、FH即可解决问题.
解答 解:(1)如图1中,连接OD,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=1,∠C=90°
在Rt△ODC中,∵∠C=90°,OC=2,CD=1,
∴OD=$\sqrt{O{C}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
故答案为$\sqrt{5}$.
(2)如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.
∵∠FBE=∠E=∠CFB=90°,
∴四边形BECF是矩形,
∴BF=CF=$\frac{1}{2}$,CF=BE=$\frac{\sqrt{3}}{2}$,
在Rt△OCE中,OC=$\sqrt{O{E}^{2}+C{E}^{2}}$=$\sqrt{(1+\frac{\sqrt{3}}{2})^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
(3)如图3中,当OF⊥DE时,OF的值最大,设OF交DE于H,在OH上取一点M,使得OM=DM,连接DM.
∵FD=FE=DE=1,OF⊥DE,
∴DH=HE,OD=OE,∠DOH=$\frac{1}{2}$∠DOE=22.5°,
∵OM=DM,
∴∠MOD=∠MDO=22.5°,
∴∠DMH=∠MDH=45°,
∴DH=HM=$\frac{1}{2}$,
∴DM=OM=$\frac{\sqrt{2}}{2}$,
∵FH=$\sqrt{D{F}^{2}-D{H}^{2}}$=$\frac{\sqrt{3}}{2}$,
∴OF=OM+MH+FH=$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}+\sqrt{2}+1}{2}$.
∴OF的最大值为$\frac{\sqrt{3}+\sqrt{2}+1}{2}$.
点评 本题考查四边形综合题、勾股定理、等边三角形的性质、正方形的性质等知识,教育的关键是学会添加常用辅助线,构造直角三角形解决问题,学会在特殊位置寻找最值问题,属于中考压轴题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题

| A. | 如图1,展开后测得∠1=∠2 | B. | 如图2,展开后测得∠1=∠2且∠3=∠4 | ||
| C. | 如图3,测得∠1=∠2 | D. | 在图④中,展开后测得∠1+∠2=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于M,交DC于N,设AE=x,则图中阴影部分的面积S与x的大致图象是( )
如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于M,交DC于N,设AE=x,则图中阴影部分的面积S与x的大致图象是( )| A. | 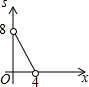 | B. | 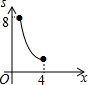 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将边长为a的正方形ABCD与边长为b的正方形ECGF(CE<AB)拼接在一起,使B、C、G三点在同一条直线上,CE在边CD上,连接AF,M为AF的中点,连接DM、CM,若ab=20,则图中阴影部分的面积为$\frac{1}{4}$a2+5.
如图,将边长为a的正方形ABCD与边长为b的正方形ECGF(CE<AB)拼接在一起,使B、C、G三点在同一条直线上,CE在边CD上,连接AF,M为AF的中点,连接DM、CM,若ab=20,则图中阴影部分的面积为$\frac{1}{4}$a2+5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com