
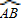 所在圆的圆心为O.车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π)
所在圆的圆心为O.车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π)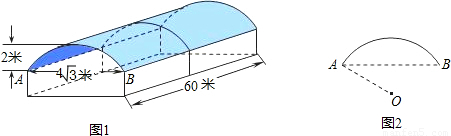
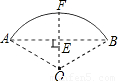 解:连接OB,过点O作OE⊥AB,垂足为E,交
解:连接OB,过点O作OE⊥AB,垂足为E,交 于F,如图,
于F,如图,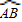 中点,
中点, AB=2
AB=2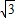 ,EF=2,
,EF=2,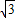 )2,
)2,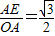 ,
,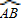 的长为
的长为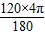 =
= π(m),
π(m), π×60=160π(平方米).
π×60=160π(平方米).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:022
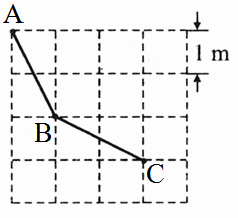
(2006·河北)如图所示是由边长为1m的正方形地砖铺设的地面示意图,小明沿图中所示的折线从A→B→C所走的路程为________m.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(09)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年河北省中考数学试卷(课标卷)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com