
【题目】居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
【答案】(1)300(2)图形见解析(3)2800
【解析】
试题分析:(1)由被调查人数=A层次的人数÷A层次人数占被调查人数的百分比,计算可得;
(2)根据D层次人数÷被调查总人数=D层次百分比,用1减去其它层次百分比可得B层次百分比,将B、C两层次百分比分别乘以被调查总人数可得B、C层次的人数,补全图形;
(3)用A、B两层次百分比之和乘以总人数4000可得.
试题解析:(1)∵90÷30%=300(人),
∴本次被抽查的居民有300人.
(2)∵D所占的百分比:30÷300=10%,
∴B所占的百分比:1﹣20%﹣30%﹣10%=40%,
∴B对应的人数:300×40%=120(人),C对应的人数:300×20%=60(人),
补全统计图,如图所示:
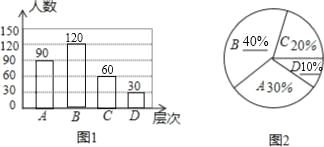
(3)∵4000×(30%+40%)=2800(人),
∴估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有2800人.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】下列有关比例中项的描述正确的有( )
(1)若a,b,c满足![]() ,则b是a,c的比例中项;
,则b是a,c的比例中项;
(2)实数b是2,8的比例中项,则b=4;
(3)如图1,点F是EG边上一点,且∠EDF=∠G,则DE是EF,EG的比例中项;
(4)如图2,四边形ABCD中,AD∥BC,两对角线相交于点O,记△AOD,△ABO,△OBC的面积分别为S1,S2,S3,则S2是S1、S3的比例中项.

A.(2)(3) B.(1)(3)(4) C.(1)(2)(3)(4) D.(1)(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=﹣![]() (x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,
(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,
(1)求A,B点的坐标;
(2)当CE:CD=1:2时,求此时抛物线C2的顶点坐标;
(3)若四边形ABCD是菱形.
①此时抛物线C2的解析式;
②点F在抛物线C2的对称轴上,且点F在第三象限,点M在抛物线C2上,点P是坐标平面内一点,是否存在以A,F,P,M为顶点的四边形与菱形ABCD相似,并且这个菱形以A为顶点的角是钝角,若存在求出点F的坐标,若不存在请说明理由.
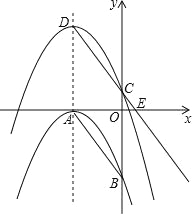
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,其中正确命题的个数为( )个.
①方差是衡量一组数据波动大小的统计量;②影响超市进货决策的主要统计量是众数;③折线统计图反映一组数据的变化趋势;④水中捞月是必然事件.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BE=CD

(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com