
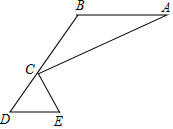
 如图,AB∥DE,C为BD上一点,∠A=∠BCA,∠E=∠ECD,求证:CE⊥CA.
如图,AB∥DE,C为BD上一点,∠A=∠BCA,∠E=∠ECD,求证:CE⊥CA. 科目:初中数学 来源: 题型:选择题
| A. | 要了解某大洋的海水污染质量情况,宜采用全面调查方式 | |
| B. | 如果有一组数据为5,3,6,4,2,那么它的中位数是6 | |
| C. | 为了解怀化市6月15日到19日的气温变化情况,应制作折线统计图 | |
| D. | “打开电视,正在播放怀化新闻节目”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
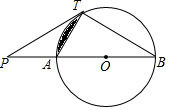 如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.
如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
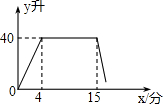 妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:
妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
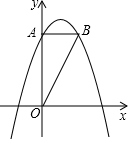 如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.
如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com