
【题目】如图,在平面直角坐标系中,一次函数y=![]() x+2的图象与y轴交于A点,与x轴交于B点,⊙P的半径为
x+2的图象与y轴交于A点,与x轴交于B点,⊙P的半径为![]() ,其圆心P在x轴上运动.
,其圆心P在x轴上运动.
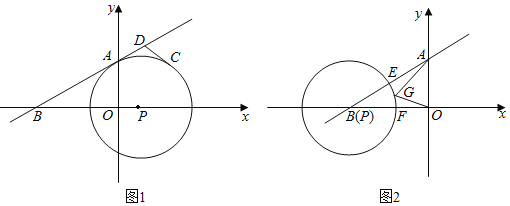
(1)如图1,当圆心P的坐标为(1,0)时,求证:⊙P与直线AB相切;
(2)在(1)的条件下,点C为⊙P上在第一象限内的一点,过点C作⊙P的切线交直线AB于点D,且∠ADC=120°,求D点的坐标;
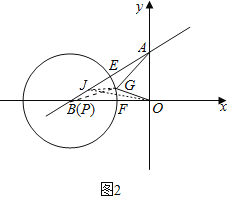
(3)如图2,若⊙P向左运动,圆心P与点B重合,且⊙P与线段AB交于E点,与线段BO相交于F点,G点为弧EF上一点,直接写出![]() AG+OG的最小值 .
AG+OG的最小值 .
【答案】(1)见解析;(2)D(![]() ,
,![]() +2);(3)
+2);(3)![]() .
.
【解析】
(1)连接PA,先求出点A和点B的坐标,从而求出OA、OB、OP和AP的长,即可确定点A在圆上,根据相似三角形的判定定理证出△AOB∽△POA,根据相似三角形的性质和等量代换证出PA⊥AB,即可证出结论;
(2)连接PA,PD,根据切线长定理可求出∠ADP=∠PDC=![]() ∠ADC=60°,利用锐角三角函数求出AD,设D(m,
∠ADC=60°,利用锐角三角函数求出AD,设D(m,![]() m+2),根据平面直角坐标系中任意两点之间的距离公式求出m的值即可;
m+2),根据平面直角坐标系中任意两点之间的距离公式求出m的值即可;
(3)在BA上取一点J,使得BJ=![]() ,连接BG,OJ,JG,根据相似三角形的判定定理证出△BJG∽△BGA,列出比例式可得GJ=
,连接BG,OJ,JG,根据相似三角形的判定定理证出△BJG∽△BGA,列出比例式可得GJ=![]() AG,从而得出
AG,从而得出![]() AG+OG=GJ+OG,设J点的坐标为(n,
AG+OG=GJ+OG,设J点的坐标为(n,![]() n+2),根据平面直角坐标系中任意两点之间的距离公式求出n,从而求出OJ的长,然后根据两点之间线段最短可得GJ+OG≥OJ,即可求出结论.
n+2),根据平面直角坐标系中任意两点之间的距离公式求出n,从而求出OJ的长,然后根据两点之间线段最短可得GJ+OG≥OJ,即可求出结论.
(1)证明:如图1中,连接PA.
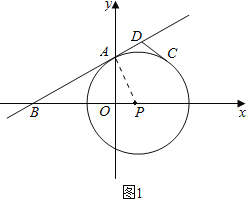
∵一次函数y=![]() x+2的图象与y轴交于A点,与x轴交于B点,
x+2的图象与y轴交于A点,与x轴交于B点,
∴A(0,2),B(﹣4,0),
∴OA=2,OB=4,
∵P(1,0),
∴OP=1,
∴OA2=OBOP,AP=![]()
∴![]() =
=![]() ,点A在圆上
,点A在圆上
∵∠AOB=∠AOP=90°,
∴△AOB∽△POA,
∴∠OAP=∠ABO,
∵∠OAP+∠APO=90°,
∴∠ABO+∠APO=90°,
∴∠BAP=90°,
∴PA⊥AB,
∴AB是⊙P的切线.
(2)如图1﹣1中,连接PA,PD.

∵DA,DC是⊙P的切线,∠ADC=120°,
∴∠ADP=∠PDC=![]() ∠ADC=60°,
∠ADC=60°,
∴∠APD=30°,
∵∠PAD=90°
∴AD=PAtan30°=![]() ,
,
设D(m,![]() m+2),
m+2),
∵A(0,2),
∴m2+(![]() m+2﹣2)2=
m+2﹣2)2=![]() ,
,
解得m=±![]() ,
,
∵点D在第一象限,
∴m=![]() ,
,
∴D(![]() ,
,![]() +2).
+2).
(3)在BA上取一点J,使得BJ=![]() ,连接BG,OJ,JG.
,连接BG,OJ,JG.
∵OA=2,OB=4,∠AOB=90°,
∴AB=![]() =
=![]() =2
=2![]() ,
,
∵BG=![]() ,BJ=
,BJ=![]() ,
,
∴BG2=BJBA,
∴![]() =
=![]() ,
,
∵∠JBG=∠ABG,
∴△BJG∽△BGA,
∴![]() =
=![]() =
=![]() ,
,
∴GJ=![]() AG,
AG,
∴![]() AG+OG=GJ+OG,
AG+OG=GJ+OG,
∵BJ=![]() ,设J点的坐标为(n,
,设J点的坐标为(n,![]() n+2),点B的坐标为(-4,0)
n+2),点B的坐标为(-4,0)
∴(n+4)2+(![]() n+2)2=
n+2)2=![]() ,
,
解得:n=-3或-5(点J在点B右侧,故舍去)
∴J(﹣3,![]() ),
),
∴OJ=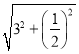 =
=![]()
∵GJ+OG≥OJ,
∴![]() AG+OG≥
AG+OG≥![]() ,
,
∴![]() AG+OG的最小值为
AG+OG的最小值为![]() .
.
故答案为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校1000名学生中,随机抽取部分学生进行问卷调查(每名学生只能从A、B、C、D中选择一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.



A:踢毽子 B:乒乓球 C:篮球 D:跳绳
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,求表示区域D的扇形圆心角的度数;
(3)全校学生中喜欢篮球的人数大约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
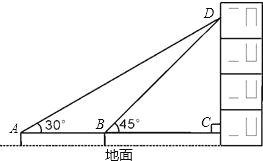
【题目】在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1米,参考数据:![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
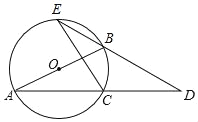
【题目】如图,AB是⊙O的直径,D是弦AC的延长线上一点,且CD=AC,DB的延长线交⊙O于点E.
(1)求证:CD=CE;
(2)连结AE,若∠D=25°,求∠BAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有标号分别为1、2、3、4、5的5个小球,这些球除标号外都相同.
(1)从袋中任意摸出一个球,摸到标号为偶数的概率是 ;
(2)先从袋中任意摸出一个球后不放回,将球上的标号作为十位上的数字,再从袋中任意摸出一个球,将球上的标号作为个位上的数字,请用画树状图或列表的方法求组成的两位数是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
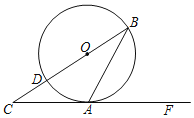
【题目】如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线CF交BD延长线于点C.
(Ⅰ)若∠C=25°,求∠BAF的度数;
(Ⅱ)若AB=AC,CD=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等腰![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、点
、点![]() .
.
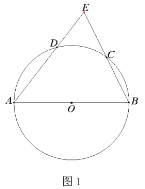
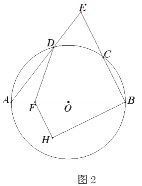
(1)如图1,求证:点![]() 为弧
为弧![]() 的中点;
的中点;
(2)如图2,点![]() 为直径
为直径![]() 上一点,过点
上一点,过点![]() 作
作![]() ,交过点
,交过点![]() 且垂直于
且垂直于![]() 的直线于点
的直线于点![]() ,连接
,连接![]() ,
,![]() ,设
,设![]()
![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
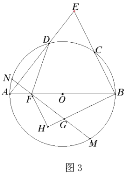
(3)如图3,在(2)的条件下,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]()
![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
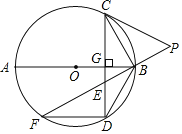
【题目】如图,AB为⊙O的直径,CD⊥AB于点G,E是CD上一点,且BE=DE,延长EB至点P,连接CP,使PC=PE,延长BE与⊙O交于点F,连结BD,FD.
(1)连结BC,求证:△BCD≌△DFB;
(2)求证:PC是⊙O的切线;
(3)若tanF=![]() ,AG﹣BG=
,AG﹣BG=![]() ,求ED的值.
,求ED的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com