
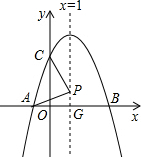
 如图,抛物线y=-x2+2x+3交x轴于点A、B,交y轴于C,其对称轴为x=1,点P为直线x=1上一点,当PA=PC时,求点P的坐标.
如图,抛物线y=-x2+2x+3交x轴于点A、B,交y轴于C,其对称轴为x=1,点P为直线x=1上一点,当PA=PC时,求点P的坐标. 分析 首先求出直线AC的解析式,再求出线段AC的垂直平分线的解析式,该直线与对称轴的交点就是所求的点P.
解答 解:由题意点 A(-1,0),C(0,3),
A(-1,0),C(0,3),
设直线AC 解析式为y=kx+b,
则有$\left\{\begin{array}{l}{-k+b=0}\\{b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$,
∴直线AC解析式为y=3x+3,
∴线段AC中点坐标(-$\frac{1}{2}$,$\frac{3}{2}$),
线段AC的中垂线解析式为y=-$\frac{1}{3}$x+$\frac{4}{3}$,
当x=1时,y=1,
∴点P坐标为(1,1).
点评 本题考查抛物线与x轴的交点、一次函数等知识,解题的关键是灵活应用待定系数法确定函数解析式,学会利用一次函数解决实际问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
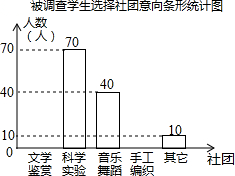 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 文学鉴赏 | 科学实验 | 音乐舞蹈 | 手工编织 | 其他 |
| 所占百分比 | a | 35% | b | 10% | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com