
分析 分三种情况①PA=PB,②AB=AP,③AB=PB,前两种情况m的值就是A和B的横坐标,再根据勾股定理可求出.
解答 解:设P(m,$\frac{1}{2}$m+2),
因为A、B的坐标为(-2,0),(4,0),
①当PA=PB时,则m=$\frac{-2+4}{2}$=1,
故有一个P点;
②当AB=AP时,则(m+2)2+($\frac{1}{2}$m+2)2=(4+2)2,
解得m=-2±$\frac{2\sqrt{165}}{5}$,
故有两个P点;
③当AB=PB时,则(m-4)2+($\frac{1}{2}$m+2)2=62
解得:m=$\frac{14±2\sqrt{129}}{5}$,
故有两个P点;
故答案为:5.
点评 本题考查一次函数图象上点的坐标特征和等腰三角形的性质,注意本题要分三种情况讨论,不要漏解.


科目:初中数学 来源: 题型:填空题
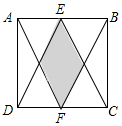 如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积是$\frac{1}{4}$.
如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积是$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
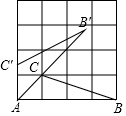 如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )
如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )| A. | $\frac{π}{2}$ | B. | π | C. | 6π | D. | 7π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
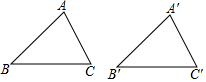 ①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.
①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com