
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为提高学生的计算能力,我县某学校八年级在元旦之前组织了一次数学速算比赛。速算规则如下:速算试题形式为计算题,共20道题,答对一题得5分,不答或错一题倒扣1分.小明代表班级参加了这次比赛,请解决下列问题:
(1)如果小明最后得分为70分,那么他计算对了多少道题?
(2)小明的最后得分可能为90分吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品的生产流水线每小时生产100件产品,生产前没有产品积压,生产3h后安排工人装箱,若每小时装产品150件,未装箱的产品数量y是时间t的函数,那么,这个函数的大致图象只能是下图中的( )
A. 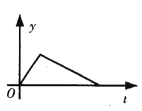 B.
B. 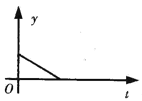
C. 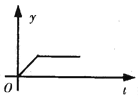 D.
D. 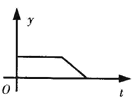
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(a),(b),(c)所示,点E、D分别是正![]() 、正四边形ABCM,正五边形ABCMN钟以C点为顶点的相邻两边上的点,且
、正四边形ABCM,正五边形ABCMN钟以C点为顶点的相邻两边上的点,且![]() ,DB交AE于点P.
,DB交AE于点P.
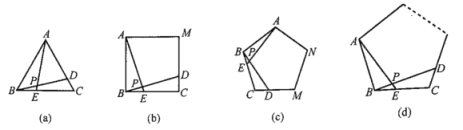
(1)在图(a)中,求![]() 的度数.
的度数.
(2)在图(b)中,![]() 的度数为________,图(c)中,
的度数为________,图(c)中,![]() 的度数为________.
的度数为________.
(3)根据前面探索,你能否将本题推广到一般的正n边形情况.若能,写出推广问题和结论;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于![]() EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
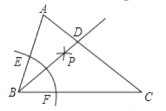
A.∠ADB=∠ABCB.AB=BDC.AC=AD+BDD.∠ABD=∠BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用![]() 元购进
元购进![]() 两种新型护服台灯共
两种新型护服台灯共![]() 盏,这两种台灯的进价、标价如下表所示:
盏,这两种台灯的进价、标价如下表所示:
价格 |
|
|
进价(元/盏) |
|
|
标价(元/盏) |
|
|
(1)![]() 两种新型护眼台灯分别购进多少盏?
两种新型护眼台灯分别购进多少盏?
(2)若![]() 型护眼灯按标价的
型护眼灯按标价的![]() 折出售,
折出售,![]() 型护眼灯按标价的
型护眼灯按标价的![]() 折出售,那么这批台灯全部售完后,商场共获利
折出售,那么这批台灯全部售完后,商场共获利![]() 元,请求出表格中
元,请求出表格中![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公交车行驶在笔直的公路上,这条路上有![]() ,
,![]() ,
,![]() ,
,![]() 四个站点,每相邻两站之间的距离为5千米,从
四个站点,每相邻两站之间的距离为5千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在
站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在![]() ,
,![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.

(1)问第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
(2)若第一班上行车行驶时间为![]() 小时,第一班上行车与第一班下行车之间的距离为
小时,第一班上行车与第一班下行车之间的距离为![]() 千米,求
千米,求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)一乘客前往![]() 站办事,他在
站办事,他在![]() ,
,![]() 两站间的
两站间的![]() 处(不含
处(不含![]() ,
,![]() 站),刚好遇到上行车,
站),刚好遇到上行车,![]() 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到
千米,此时,接到通知,必须在35分钟内赶到,他可选择走到![]() 站或走到
站或走到![]() 站乘下行车前往
站乘下行车前往![]() 站.若乘客的步行速度是5千米/小时,求
站.若乘客的步行速度是5千米/小时,求![]() 满足的条件.
满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发, 到达目的地后停止,设慢车行驶时间为 x 小时,两车之间的距离为 y 千米,两者的关系如图 所示:
(1)两车出发 小时后相遇;
(2)求快车和慢车的速度;
(3)求线段 BC 所表示的 y 与 x 的 关系式,并求两车相距 300 千米时的时间.
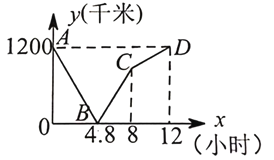
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com