
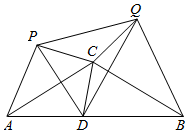
 如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:分析 ①由折叠直接得到结论;
②由折叠的性质求出∠ACP+∠BCQ=120°,再用周角的意义求出∠PCQ=120°;
③先作出△PCQ的边PC上的高,用三角函数求出QE=$\sqrt{3}$CQ,得到S△PCQ=$\frac{\sqrt{3}}{2}$CD2,判断出△PCQ面积最小时,点D的位置,求出最小的CD=CF,即可;
④先判断出△APD是等边三角形,△BDQ是等边三角形,再求出∠PDQ=60°,即可.
解答 解:①∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴CP=CD=CQ,
∴①正确;
②∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴∠ACP=∠ACD,∠BCQ=∠BCD,
∴∠ACP+∠BCQ=∠ACD+∠BCD=∠ACB=120°,
∴∠PCQ=360°-(∠ACP+BCQ+∠ACB)=360°-(120°+120°)=120°,
∴∠PCQ的大小不变;
∴②正确;
③如图,
过点Q作QE⊥PC交PC延长线于E,
∵∠PCQ=120°,
∴∠QCE=60°,
在Rt△QCE中,sin∠QCE=$\frac{QE}{CQ}$,
∴QE=CQ×sin∠QCE=CQ×sin60°=$\frac{\sqrt{3}}{2}$CQ,
∵CP=CD=CQ
∴S△PCQ=$\frac{1}{2}$CP×QE=$\frac{1}{2}$CP×$\frac{\sqrt{3}}{2}$CQ=$\frac{\sqrt{3}}{4}$CD2,
∴CD最短时,S△PCQ最小,
即:CD⊥AB时,CD最短,
过点C作CF⊥AB,此时CF就是最短的CD,
∵AC=BC=4,∠ACB=120°,
∴∠ABC=30°,
∴CF=$\frac{1}{2}$BC=2,
即:CD最短为2,
∴S△PCQ最小=$\frac{\sqrt{3}}{4}$CD2=$\frac{\sqrt{3}}{4}$×22=$\sqrt{3}$,
∴③错误,
④∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴AD=AP,∠DAC=∠PAC,
∵∠DAC=30°,
∴∠APD=60°,
∴△APD是等边三角形,
∴PD=AD,∠ADP=60°,
同理:△BDQ是等边三角形,
∴DQ=BD,∠BDQ=60°,
∴∠PDQ=60°,
∵当点D在AB的中点,
∴AD=BD,
∴PD=DQ,
∴△DPQ是等边三角形.
∴④正确,
故答案为:①②④.
点评 此题是几何变换综合题,主要考查了折叠的性质,等腰三角形的性质,等边三角形的判定,锐角三角函数,极值的确定,三角形的面积公式,解本题的关键是判断出∠PCQ=120°是个定值;(其实这个题目中还有∠PDQ=60°也是定值),解本题的难点是确定出△PCQ面积最小时,点D的位置.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学课上郝老师要求王旺在黑板上完成,解不等式:$\frac{2x-1}{3}$-$\frac{9x+2}{6}$≤1并把解集表示在数轴上,下面是他的解题过程:
数学课上郝老师要求王旺在黑板上完成,解不等式:$\frac{2x-1}{3}$-$\frac{9x+2}{6}$≤1并把解集表示在数轴上,下面是他的解题过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
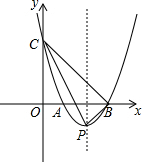 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
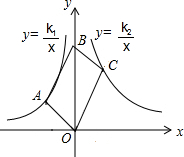 如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )
如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )| A. | -2k1 | B. | 2k2 | C. | k1+k2 | D. | k2-k1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com