
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的解析式.
(2)如图2,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 点是
点是![]() 轴上一个动点,过点
轴上一个动点,过点![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,当点
,当点![]() 、
、![]() 、
、![]() 、
、![]() 四个点组成的四边形是平行四边形时,求此时
四个点组成的四边形是平行四边形时,求此时![]() 点坐标.
点坐标.
(3)如图3,连接![]() 和
和![]() ,
,![]() 点是抛物线上一个动点,连接
点是抛物线上一个动点,连接![]() ,当
,当![]() 时,求
时,求![]() 点的坐标.
点的坐标.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的盒子中,分别装有除颜色外其它完全相同的小球,其中,甲盒子装有2个白球,1个红球;乙盒子装有2个红球,1个白球.
(1)将甲盒子摇匀后,随机取出一个小球,求小球是白色的概率;
(2)小华和同桌商定:将两个盒子摇匀后,各随机摸出一个小球.若颜色相同,则小华获胜;若颜色不同,则同桌获胜,请用列表法或画出树状图的方法说明谁赢的可能性大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋中装有2个红球和2个绿球.
(1)先从袋中摸出1个球后放回,混合均匀后再摸出1个球,求两次摸到的球中有1个绿球和1个红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出个球,则两次摸到的球中有1个绿球和1个红球的概率是 .(直接填答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为( )
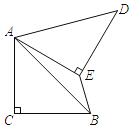
A.100°B.120°C.135°D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,对称轴为直线x=1.以下结论:①2a>-b;②4a+2b+c>0;③m(am+b)>a+b(m是大于1的实数);④3a+c<0其中正确结论的个数为( )
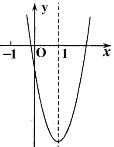
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直线![]() 上有相距
上有相距![]() 的两点
的两点![]() 和
和![]() (点
(点![]() 在点
在点![]() 的右侧),以
的右侧),以![]() 为圆心作半径为
为圆心作半径为![]() 的圆,过点
的圆,过点![]() 作直线
作直线![]() .将
.将![]() 以
以![]() 的速度向右移动(点
的速度向右移动(点![]() 始终在直线
始终在直线![]() 上),则
上),则![]() 与直线
与直线![]() 在______秒时相切.
在______秒时相切.
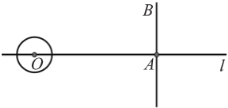
A.3B.3.5C.3或4D.3或3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为美化中心城区环境,政府计划在长为30米,宽为20米的矩形场地![]() 上修建公园.其中要留出宽度相等的三条小路,且两条与
上修建公园.其中要留出宽度相等的三条小路,且两条与![]() 平行,另一条与
平行,另一条与![]() 平行,其余部分建成花圃.
平行,其余部分建成花圃.
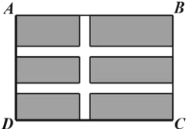
(1)若花圃总面积为448平方米,求小路宽为多少米?
(2)已知某园林公司修建小路的造价![]() (元)和修建花圃的造价
(元)和修建花圃的造价![]() (元)与修建面积
(元)与修建面积![]() (平方米)之间的函数关系分别为
(平方米)之间的函数关系分别为![]() 和
和![]() .若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低?
.若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
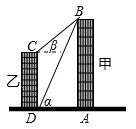
【题目】如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
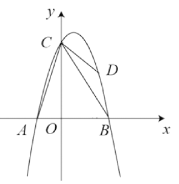
如图,抛物线![]() 经过点A(-2,0),B(4,0)两点,与
经过点A(-2,0),B(4,0)两点,与![]() 轴交于点C,点D是抛物线上一个动点,设点D的横坐标为
轴交于点C,点D是抛物线上一个动点,设点D的横坐标为![]() .连接AC,BC,DB,DC,
.连接AC,BC,DB,DC,
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若点M是![]() 轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com