
ЁОЬтФПЁПШчЭМЃЌвбжЊAЁЂBСНЕидкЪ§жсЩЯЯрОр20УзЃЌAЕидкЪ§жсЩЯБэЪОЕФЕуЮЊ-8ЃЌаЁЮкЙъДгAЕиГіЗЂбиЪ§жсЭљBЕиЗНЯђЧАНјЃЌЕквЛДЮЧАНј1УзЃЌЕкЖўДЮКѓЭЫ2УзЃЌЕкШ§ДЮдйЧАНј3УзЃЌЕкЫФДЮгжКѓЭЫ4УзЃЌЁЁЃЌАДДЫЙцТЩааНјЃЌЃЈЪ§жсЕФвЛИіЕЅЮЛГЄЖШЕШгк1УзЃЉ
![]()
ЃЈ1ЃЉЧѓBЕидкЪ§жсЩЯБэЪОЕФЪ§ЃЛ
ЃЈ2ЃЉШєBЕидкдЕуЕФзѓВрЃЌОЙ§ЕкЮхДЮааНјКѓаЁЮкЙъЕНДяЕуPЃЌЕкСљДЮааНјКѓЕНДяЕуQЃЌдђЕуPКЭЕуQЕНЕуAЕФОрРыЯрЕШТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєBЕидкдЕуЕФгвВрЃЌФЧУДОЙ§30ДЮааНјКѓЃЌаЁЮкЙъЕНДяЕФЕугыЕуBжЎМфЕФОрРыЪЧЖрЩйУзЃП
ЁОД№АИЁПЃЈ1ЃЉ12Лђ-28ЃЛЃЈ2ЃЉЯрЕШЃЛЃЈ3ЃЉ70Уз.
ЁОНтЮіЁП
ЃЈ1ЃЉЕНAЕиОрРыЮЊ20ЕФЕугаСНИіЃЌЗжБ№ЮЛгкAЕузѓВрЁЂгвВр.вРОнЪ§жсСНЕуОрРыМДПЩЧѓЕУЕуBзјБъ
ЃЈ2ЃЉЪ§жсЩЯЕуЕФвЦЖЏЙцТЩЪЧЁАзѓМѕгвМгЁБЃЎвРОнЙцТЩМЦЫуЗжБ№ЧѓГіЕуPЁЂQЯрЖдAЕувЦЖЏЕФОрРыМДПЩЕУЕНД№АИ
ЃЈ3ЃЉИљОн100ЮЊХМЪ§ПЩЕУдкЪ§жсЩЯБэЪОЕФЪ§ЃЌдйИљОнСНЕуМфЕФОрРыЙЋЪНМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Д№ЃК![]() ЕидкЪ§жсЩЯБэЪОЕФЪ§ЪЧ12Лђ
ЕидкЪ§жсЩЯБэЪОЕФЪ§ЪЧ12Лђ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉСюаЁЮкЙъДгAЕиГіЗЂЃЌЧАНјЮЊЁА+ЁБЃЌКѓЭЫЮЊЁА-ЁБЃЌдђЃК
ЕкЮхДЮааНјКѓЯрЖдAЕФЮЛжУЮЊЃК![]() ЃЌ
ЃЌ
ЕкСљДЮааНјКѓЯрЖдAЕФЮЛжУЮЊЃК![]() ЃЌ
ЃЌ
вђЮЊЕу![]() ЁЂ
ЁЂ![]() гы
гы![]() ЕуЕФОрРыЖМЪЧ3УзЃЌ
ЕуЕФОрРыЖМЪЧ3УзЃЌ
ЫљвдЕу![]() ЁЂЕу
ЁЂЕу![]() ЕН
ЕН![]() ЕиЕФОрРыЯрЕШЃЛ
ЕиЕФОрРыЯрЕШЃЛ
ЃЈ3ЃЉШє![]() ЕидкдЕуЕФгвВрЃЌЧАНјЮЊЁА+ЁБЃЌКѓЭЫЮЊЁА-ЁБЃЌ
ЕидкдЕуЕФгвВрЃЌЧАНјЮЊЁА+ЁБЃЌКѓЭЫЮЊЁА-ЁБЃЌ
дђЕБ![]() ЮЊ100ЪБЃЌЫќдкЪ§жсЩЯБэЪОЕФЪ§ЮЊЃК
ЮЊ100ЪБЃЌЫќдкЪ§жсЩЯБэЪОЕФЪ§ЮЊЃК
![]() ЃЌ
ЃЌ
ЁпBЕуБэЪОЕФЮЊ12.
ЁрABЕФОрРыЮЊ![]() ЃЈУз
ЃЈУз![]() ЃЎ
ЃЎ
Д№ЃКаЁЮкЙъЕНДяЕФЕугыЕу![]() жЎМфЕФОрРыЪЧ70УзЃЎ
жЎМфЕФОрРыЪЧ70УзЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
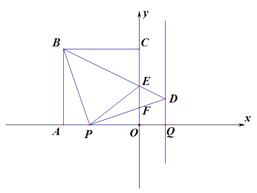
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ![]() е§ЗНаЮOABCЕФБпOAЁЂOCдкзјБъжсЩЯ.дк
е§ЗНаЮOABCЕФБпOAЁЂOCдкзјБъжсЩЯ.дк![]() жсЩЯЯпЖЮ
жсЩЯЯпЖЮ![]() ЃЈQдкAЕФгвБпЃЉЃЌPДгAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђOдЫЖЏЃЌЕБЕуPЕНДяЕуOЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЮЊ
ЃЈQдкAЕФгвБпЃЉЃЌPДгAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђOдЫЖЏЃЌЕБЕуPЕНДяЕуOЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЮЊ![]() .СЌНгPBЃЌЙ§PзїPBЕФДЙЯпЃЌЙ§Qзї
.СЌНгPBЃЌЙ§PзїPBЕФДЙЯпЃЌЙ§Qзї![]() жсЕФДЙЯпЃЌСНДЙЯпЯрНЛгкЕуD.СЌНгBDНЛ
жсЕФДЙЯпЃЌСНДЙЯпЯрНЛгкЕуD.СЌНгBDНЛ![]() жсгкЕуEЃЌСЌНгPDНЛ
жсгкЕуEЃЌСЌНгPDНЛ![]() жсгкЕуFЃЌСЌНгPE.
жсгкЕуFЃЌСЌНгPE.
ЃЈ1ЃЉЧѓЁЯPBDЕФЖШЪ§.
ЃЈ2ЃЉЩшЁїPOEЕФжмГЄЮЊ![]() ЃЌЬНЫї
ЃЌЬНЫї![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГі
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГі![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ЃЈ3ЃЉСю![]() ЃЌЕБЁїPBEЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЁїEFDЕФУцЛ§.
ЃЌЕБЁїPBEЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЁїEFDЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЪЧЕШБпШ§НЧаЮЃЎ
ЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌЕуEдкЯпЖЮABЩЯЃЌЕуDдкЩфЯпCBЩЯЃЌЧвED=ECЃЎНЋЁїBCEШЦЕуCЫГЪБеыа§зЊ60ЁужСЁїACFЃЌСЌНгEFЃЎВТЯыЯпЖЮABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЃЛ
ЃЈ2ЃЉЕуEдкЯпЖЮBAЕФбгГЄЯпЩЯЃЌЦфЫќЬѕМўгыЃЈ1ЃЉжавЛжТЃЌЧыдкЭМЃЈ2ЃЉЕФЛљДЁЩЯНЋЭМаЮВЙГфЭъећЃЌВЂВТЯыЯпЖЮABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉЧыбЁдёЃЈ1ЃЉЛђЃЈ2ЃЉжаЕФвЛИіВТЯыНјаажЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§жсЩЯOЁЂAСНЕуЖдгІЕФЪ§ЮЊ0ЁЂ10ЃЌQЮЊЪ§жсЩЯвЛЕуЃЎ
ЃЈ1ЃЉQЮЊOAЯпЖЮЕФжаЕуЃЈМДЕуQЕНЕуOКЭЕуAЕФОрРыЯрЕШЃЉЃЌЕуQЖдгІЕФЪ§ЮЊЁЁЁЁЁЁЁЁ ЃЎ
ЃЈ2ЃЉЪ§жсЩЯгаЕу QЃЌЪЙ QЕНOЁЂAЕФОрРыжЎКЭЮЊ20ЃЌЕуQЖдгІЕФЪ§ЮЊЁЁЁЁЁЁЁЁЃЎ
ЃЈ3ЃЉШєЕуQЕуБэЪО8ЃЌЕуMвдУПУыжг5ИіЕЅЮЛЕФЫйЖШДгOЕуЯђгвдЫЖЏЃЌЕуNвдУПУыжг1ИіЕЅЮЛЕФЫйЖШДгAЕуЯђгвдЫЖЏЃЌtУыКѓга QM= QNЃЌЧѓЪБМфtЕФжЕt=ЁЁЁЁЁЁЁЁ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
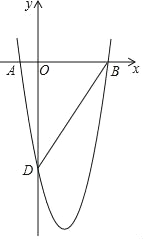
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=ax2+bxЉ4![]() ЕФЭМЯѓОЙ§AЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉСНЕуЃЌгкyжсНЛгкЕуDЃЎ
ЕФЭМЯѓОЙ§AЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉСНЕуЃЌгкyжсНЛгкЕуDЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉвбжЊЕуCЃЈ3ЃЌmЃЉдкетИіЖўДЮКЏЪ§ЕФЭМЯѓЩЯЃЌСЌНгBCЃЌЕуPЮЊХзЮяЯпЩЯвЛЕуЃЌЧвЁЯCBP=60ЁуЃЎ
ЂйЧѓЁЯOBDЕФЖШЪ§ЃЛ
ЂкЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГзЈвЕЛЇвЊГіЪл300жЛбђЃЌЯждкЪаГЁЩЯбђЕФМлИёЮЊУПЧЇПЫ11дЊЃЌЮЊСЫЙРМЦет300жЛбђФмТєЖрЩйЧЎЃЌЪдЮЪЃК
ЃЈ1ЃЉЖдгкЩЯЪіЮЪЬтФуШЯЮЊЪЪгУ___________.ЃЈЬюЁАЦеВщЁБЛђЁАГщбљЕїВщЁБЃЉ
ЃЈ2ЃЉИУзЈвЕЛЇДгПкЫцЛњГщШЁСЫ5жЛбђЃЌГЦЕУЫќУЧЕФжЪСПЃЈЕЅЮЛЃКЧЇПЫЃЉШчЯТЃК26ЃЌ31ЃЌ32 ЃЌ36ЃЌ37
ЂйдкетИіЮЪЬтжаЃЌзмЬхЁЂИіЬхКЭбљБОИїЪЧ___________ЃЌ___________ЃЌ___________.
ЂкЭЈЙ§ЩЯЪіЪ§ОнЃЌФуФмЙРЫуГіет300жЛбђФмТєЖрЩйЧЎТ№ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌACЮЊЖдНЧЯпЃЌEЮЊABЩЯвЛЕуЃЌЙ§ЕуEзїEFЁЮADЃЌгыACЁЂDCЗжБ№НЛгкЕуGЃЌFЃЌHЮЊCGЕФжаЕуЃЌСЌНгDEЃЌEHЃЌDHЃЌFHЃЎЯТСаНсТлЃК
ЂйEG=DFЃЛЂкЁЯAEH+ЁЯADH=180 ЃЛЂлЁїEHFЁеЁїDHCЃЛЂмШє![]() ЃЌдђ3SЁїEDH=13SЁїDHCЃЌЦфжаНсТле§ШЗЕФга___________ЃЎ
ЃЌдђ3SЁїEDH=13SЁїDHCЃЌЦфжаНсТле§ШЗЕФга___________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУ![]() жНИДгЁЮФМўЃЌдкМзИДгЁЕъВЛЙмвЛДЮИДгЁЖрЩйвГЃЌУПвГЪеЗб0.1дЊ.дкввИДгЁЕъИДгЁЭЌбљЕФЮФМўЃЌвЛДЮИДгЁвГЪ§ВЛГЌЙ§20ЪБЃЌУПвГЪеЗб0.12дЊЃЛвЛДЮИДгЁвГЪ§ГЌЙ§20ЪБЃЌГЌЙ§ВПЗжУПвГЪеЗб0.09дЊ.
жНИДгЁЮФМўЃЌдкМзИДгЁЕъВЛЙмвЛДЮИДгЁЖрЩйвГЃЌУПвГЪеЗб0.1дЊ.дкввИДгЁЕъИДгЁЭЌбљЕФЮФМўЃЌвЛДЮИДгЁвГЪ§ВЛГЌЙ§20ЪБЃЌУПвГЪеЗб0.12дЊЃЛвЛДЮИДгЁвГЪ§ГЌЙ§20ЪБЃЌГЌЙ§ВПЗжУПвГЪеЗб0.09дЊ.
ЩшдкЭЌвЛМвИДгЁЕъвЛДЮИДгЁЮФМўЕФвГЪ§ЮЊ![]() ЃЈ
ЃЈ![]() ЮЊЗЧИКећЪ§ЃЉ.
ЮЊЗЧИКећЪ§ЃЉ.
ЃЈ1ЃЉИљОнЬтвтЃЌЬюаДЯТБэЃК
вЛДЮИДгЁвГЪ§ЃЈвГЃЉ | 5 | 10 | 20 | 30 | Ё |
МзИДгЁЕъЪеЗбЃЈдЊЃЉ |
| 2 | Ё | ||
ввИДгЁЕъЪеЗбЃЈдЊЃЉ |
|
| Ё |
ЃЈ2ЃЉЩшдкМзИДгЁЕъИДгЁЪеЗб![]() дЊЃЌдкввИДгЁЕъИДгЁЪеЗб
дЊЃЌдкввИДгЁЕъИДгЁЪеЗб![]() дЊЃЌЗжБ№аДГі
дЊЃЌЗжБ№аДГі![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЙЫПЭдкФФМвИДгЁЕъИДгЁЛЈЗбЩйЃПЧыЫЕУїРэгЩ.
ЪБЃЌЙЫПЭдкФФМвИДгЁЕъИДгЁЛЈЗбЩйЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуPЪЧОиаЮABCDБпABЩЯЕФШЮвтвЛЕуЃЈгыЕуAЁЂBВЛжиКЯЃЉ
ЃЈ1ЃЉШчЭМЂйЃЌЯжНЋЁїPBCбиPCЗелЕУЕНЁїPECЃЛдйдкADЩЯШЁвЛЕуFЃЌНЋЁїPAFбиPFЗелЕУЕНЁїPGFЃЌВЂЪЙЕУЩфЯпPEЁЂPGжиКЯЃЌЪдЮЪFGгыCEЕФЮЛжУЙиЯЕШчКЮЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉжаЃЌШчЭМЂкЃЌСЌНгFCЃЌШЁFCЕФжаЕуHЃЌСЌНгGHЁЂEHЃЌЧыФуЬНЫїЯпЖЮGHКЭЯпЖЮEHЕФДѓаЁЙиЯЕЃЌВЂЫЕУїФуЕФРэгЩЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌЗжБ№дкADЁЂBCЩЯШЁЕуFЁЂCЁЏЃЌЪЙЕУЁЯAPF=ЁЯBPCЁЏЃЌгыЃЈ1ЃЉжаЕФВйзїЯрРрЫЦЃЌМДНЋЁїPAFбиPFЗелЕУЕНЁїPFGЃЌВЂНЋЁї![]() би
би![]() ЗелЕУЕНЁї
ЗелЕУЕНЁї![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШЁ
ЃЌШЁ![]() ЕФжаЕуHЃЌСЌНгGHЁЂEHЃЌЪдЮЪЃЈ2ЃЉжаЕФНсТлЛЙГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЎ
ЕФжаЕуHЃЌСЌНгGHЁЂEHЃЌЪдЮЪЃЈ2ЃЉжаЕФНсТлЛЙГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com