
【题目】如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM、ON分别是∠AOC、∠AOB的平分线,∠MON=56°.
⑴ ∠COD与∠AOB相等吗?请说明理由;
⑵ 求∠BOC的度数;
⑶ 求∠AOB与∠AOC的度数.
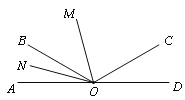
【答案】(1)∠COD=∠AOB.理由见解析;(2)∠BOC=112°;(3)∠AOC=146°.
【解析】试题分析:(1)根据题意可得∠AOC+∠AOB=180°, ∠AOC+∠COD=180°,可以根据同角的补角相等得到∠COD=∠AOB;
(2)根据OM、ON分别是∠AOC、∠AOB的平分线可得∠AOM=∠COM,∠AON=∠BON,再利用教的和差可得∠BOC=2 ∠MON;
(3)由(1)得∠COD=∠AOB, 再根据∠AOB+∠BOC+∠COD=180°可求出∠AOB的度数,然后根据平角的定义即可得到∠AOC.
解:⑴∠COD=∠AOB.理由如下:
如图 ∵点O在直线AD上
∴∠AOC+∠COD=180°
又∵∠AOC与∠AOB互补
∴∠AOC+∠AOB=180°
∴∠COD=∠AOB
⑵∵ OM、ON分别是∠AOC、∠AOB的平分线
∴∠AOM=∠COM,∠AON=∠BON
∴∠BOC=∠BOM+∠COM=∠BOM+∠AOM=(∠MON-∠BON)+(∠MON+∠AON)=2 ∠MON=112°
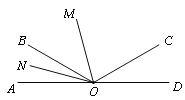
⑶由⑴得:∠COD=∠AOB
∵ ∠AOB+∠BOC+∠COD=180°
∴ ∠AOB=![]() (180°-∠BOC)=
(180°-∠BOC)=![]() (180°-112°)=34°
(180°-112°)=34°
∴ ∠AOC=180°-∠AOB=180°-34°=146°.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,E为平面内任意一点,连接DE,将线段DE绕点D顺时针旋转90°得到DG,连接EC,AG.
(1)当点E在正方形ABCD内部时, ①根依题意,在图1中补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG=2 ![]() ,求CE的长.(可在备用图中画图)
,求CE的长.(可在备用图中画图) 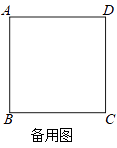
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的底边BC=8cm,且|AC﹣BC|=2cm,则腰长AC的长为( )
A. 10cm或6cm B. 10cm C. 6cm D. 8cm或6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点 F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
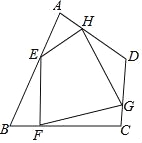
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2﹣4ax﹣5(a>0).
(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;
②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;
(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果(x﹣2)(x+3)=x2+px+q,那么p、q的值为( )
A.p=5,q=6
B.p=1,q=﹣6
C.p=1,q=6
D.p=5,q=﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com