
如图,△ABC内接于⊙O,AB=AC,BD是⊙O的直径, AD与BC交于点E,
F在DA的延长线上,且AF=AE.

(1)试判断BF与⊙O的位置关系,并说明理由;
(2)若BF=5,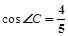 ,求⊙O的直径.
,求⊙O的直径.
(1)BF与⊙O相切 (2)⊙O的直径是
【解析】
试题分析:解:(1)BF与⊙O相切
∵ BD是直径
∴∠DAB=90°
∵AE=AF,∠BAD=∠BAF,BA=BA
∴△BAE≌△BAF
∴∠CBA=∠FBA
∵AB=AC
∴∠C=∠CBA
又∵∠D=∠C
∴∠D=∠CBA
∴∠D=∠FBA
∵∠FBA+∠F=180°-∠BAF=90°
∴∠D+∠F=90°
∴∠DBF=180°-(∠D+∠F)=90°
∴OB⊥BF
∴BF与⊙O相切
(2)∵∠D =∠C
∴c o s∠D =" c" o s∠C = 
在R t△BDF中,c o s∠D=
设BD =4x, DF =5x,则BF =3x
∵BF =5, ∴3x=5, ∴x=
∴BD ="4x" =
∴⊙O的直径是
考点:圆切线判定和三角函数
点评:该题考查学生对圆相关知识点的掌握程度,线与圆的关系、同弦所对的圆心角与圆周角的关系都是常考的知识点。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com