
【题目】如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点. 
(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
【答案】
(1)解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠ABC=30°,AB=4,
∴BD=2 ![]() ,
,
∵D是BC的中点,
∴BC=2BD=4 ![]()
(2)证明:连接OD.
∵D是BC的中点,O是AB的中点,
∴DO是△ABC的中位线,
∴OD∥AC,则∠EDO=∠CED
又∵DE⊥AC,
∴∠CED=90°,∠EDO=∠CED=90°
∴DE是⊙O的切线.
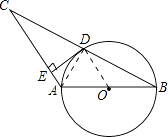
【解析】(1)根据圆周角定理求得∠ADB=90°,然后解直角三角形即可求得BD,进而求得BC即可;(2)要证明直线DE是⊙O的切线只要证明∠EDO=90°即可.
【考点精析】通过灵活运用含30度角的直角三角形和圆周角定理,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.


科目:初中数学 来源: 题型:
【题目】数轴上点![]() 对应的数为
对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,点
,点![]() 为数轴上一动点.
为数轴上一动点.
(1) AB的距离是 .
(2) ①若点![]() 到点
到点![]() 的距离比到点
的距离比到点![]() 的距离大1,点
的距离大1,点![]() 对应的数为 .
对应的数为 .
②若点![]() 其对应的数为
其对应的数为![]() ,数轴上是否存在点
,数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() ,点
,点![]() 的距离之和为8?若存在,请求出
的距离之和为8?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)当点![]() 以每秒钟
以每秒钟![]() 个单位长度从原点
个单位长度从原点![]() 向右运动时,点
向右运动时,点![]() 以每秒钟
以每秒钟![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向左运动,点
向左运动,点![]() 以每秒钟
以每秒钟![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向右运动,问它们同时出发 秒钟时,
向右运动,问它们同时出发 秒钟时,![]() (直接写出答案即可).
(直接写出答案即可).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查方式合适的是( )
A. 为了了解外地游客对岳阳楼新景区的感受,小华利用周日在汴河街随机采访了![]() 名武汉游客
名武汉游客
B. 为了了解全校学生用于做数学作业的时间,小民同学在网上通过![]() 向
向![]() 位好友做了调查
位好友做了调查
C. 为了了解“嫦娥一号”卫星零部件的状况,检测人员采用了普查的方式
D. 为了了解全国青少年儿童在阳光体育运动启动后的睡眠时间,统计人员采用了普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设计调查问卷时,下列提问是否合适?如果不合适的话应该怎样改进?
(1)你上学时使用的交通工具是
![]() .汽车
.汽车![]() .摩托车
.摩托车![]() .步行
.步行![]() .其他
.其他
(2)你对老师的教学满意吗?
![]() .比较满意
.比较满意![]() .满意
.满意![]() .非常满意.
.非常满意.
查看答案和解析>>
科目:初中数学 来源: 题型:
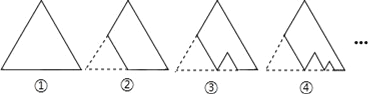
【题目】图①是一块边长为1,周长记为P1的正三角形纸板,沿图①的底边剪去一块边长为![]() 的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的
的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的![]() )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则P2018﹣P2017的值为( )
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则P2018﹣P2017的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣2x2+(m+9)x﹣6的对称轴是x=2.
(1)求抛物线表达式和顶点坐标;
(2)将该抛物线向右平移1个单位,平移后的抛物线与原抛物线相交于点A,求点A的坐标;
(3)抛物线y=﹣2x2+(m+9)x﹣6与y轴交于点C,点A关于平移后抛物线的对称轴的对称点为点B,两条抛物线在点A、C和点A、B之间的部分(包含点A、B、C) 记为图象M.将直线y=2x﹣2向下平移b(b>0)个单位,在平移过程中直线与图象M始终有两个公共点,请你写出b的取值范围 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边△ABC内的一点,且PA=5,PB=4,PC=3,将△APB绕点B逆时针旋转,得到△CQB.求: 
(1)点P与点Q之间的距离;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读资料:
如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1 , y1),B(x2 , y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A,B两点间的距离为AB= ![]() .
.
我们知道,圆可以看成到圆心的距离等于半径的点的集合,如图2,在平面直角坐标系xOy中,A (x,y)为圆上任意一点,则点A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2 , 当⊙O的半径OA为r时,⊙O的方程可写为:x2+y2=r2 .
问题拓展:
如果圆心坐标为P (a,b),半径为r,那么⊙P的方程可以写为 (x﹣a)2+(y﹣b)2=r2 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以点Q为圆心,OQ长为半径的⊙Q的方程;若不存在,说明理由.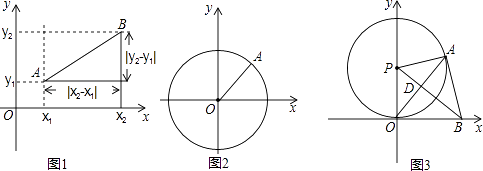
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 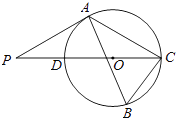
(1)求证:PA是⊙O的切线;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com