
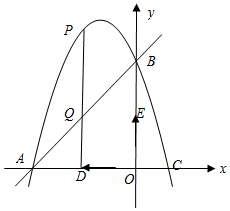
 如图,抛物线经过点A(-3,0)、B(0,3),C(1,0).
如图,抛物线经过点A(-3,0)、B(0,3),C(1,0).分析 (1)设交点式y=a(x+3)(x-1),再把B点坐标代入求出a即可得到抛物线的解析式;然后利用待定系数法直线AB的解析式;
(2)①由于D(-t,0),PD⊥x轴,则可表示出P点坐标为(-t,-t2+2t+3),所以PQ=-t2+2t+3,然后利用二次函数的性质解决问题;
②由于PQ∥OE,则PQ=OE时,四边形DOEP为平行四边形,此时四边形DOEP是正方形,即-t2+2t+3=t,然后解方程可得到满足条件的t的值;
③作EH⊥PD,如图,利用等腰三角形的性质得PH=DH,即PD=2OE,所以-t2+2t+3=2t,然后解方程可得到满足条件的t的值.
解答 解:(1)设抛物线的解析式为y=a(x+3)(x-1),
把B(0,3)代入得a•3•(-1)=3,解得a=-1,
∴抛物线的解析式为y=-(x+3)(x-1),
即y=-x2-2x+3;
设直线AB的解析式为y=kx+b,
把A(-3,0),B(0,3)代入得$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴直线AB的解析式为y=x+3;
(2)①∵D(-t,0),PD⊥x轴,
∴P(-t,-t2+2t+3),
∴PQ=-t2+2t+3=-(t-1)2+4,
∴当t=1时,PQ的长度有最大值,最大值为4;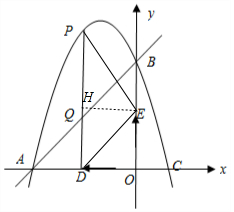
②OE=OD=t,
∵PQ∥OE,
∴PQ=OE时,四边形DOEP为平行四边形,
而OE=OD,∠DOE=90°,
∴此时四边形DOEP是正方形
即-t2+2t+3=t,解得t1=$\frac{1+\sqrt{13}}{2}$,t2=$\frac{1-\sqrt{13}}{2}$(舍去),
∴当t为$\frac{1+\sqrt{13}}{2}$时,四边形DOEP是正方形;
③存在.
作EH⊥PD,如图,
∵DE=PE,
∴PH=DH,
∴PD=2OE,
即-t2+2t+3=2t,解得t1=$\sqrt{3}$,t2=-$\sqrt{3}$(舍去),
∴当t=$\sqrt{3}$时,PE=DE.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式;灵活应用正方形的性质;理解坐标与图形性质.


科目:初中数学 来源: 题型:解答题
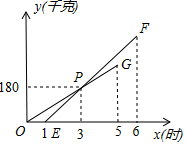 某家装公司聘请两队搬运工来搬运货物,他们都只能连续搬运5小时,甲队于某日0时开始搬运,过了1小时,乙队也开始搬运,如图,线段OG表示甲队搬运量y(千克)与时间x(时)的函数图象,线段EF表示乙队搬运量y(千克)与时间x(时)的函数图象.
某家装公司聘请两队搬运工来搬运货物,他们都只能连续搬运5小时,甲队于某日0时开始搬运,过了1小时,乙队也开始搬运,如图,线段OG表示甲队搬运量y(千克)与时间x(时)的函数图象,线段EF表示乙队搬运量y(千克)与时间x(时)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的横坐标为( )
如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的横坐标为( )| A. | 1010 | B. | 2 | C. | 1 | D. | -1006 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′,连接CC′.若∠CC′B′=32°,则∠B的大小是( )| A. | 32° | B. | 64° | C. | 77° | D. | 87° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
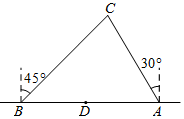 如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60($\sqrt{3}$+1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.
如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60($\sqrt{3}$+1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
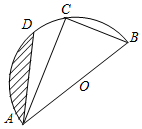 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com