
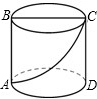
 如图所示,是一圆柱体,已知圆柱的高AB=3,底面直径BC=10,现在有一只蚂蚁想要从A处沿圆柱表面爬行到对角C处去捕食,则它爬行最短路径是( )(本题π取3).
如图所示,是一圆柱体,已知圆柱的高AB=3,底面直径BC=10,现在有一只蚂蚁想要从A处沿圆柱表面爬行到对角C处去捕食,则它爬行最短路径是( )(本题π取3).| A、13 | ||
B、3
| ||
C、
| ||
D、2
|
科目:初中数学 来源: 题型:
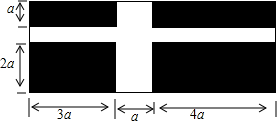 某学校欲建如图所示的草坪(阴影部分),请你计算一下,一共需要铺是设草坪多少平方米?如果每平方米草坪需100元,则学校为是设草坪一共需投资多少元?(单位:米)
某学校欲建如图所示的草坪(阴影部分),请你计算一下,一共需要铺是设草坪多少平方米?如果每平方米草坪需100元,则学校为是设草坪一共需投资多少元?(单位:米)查看答案和解析>>
科目:初中数学 来源: 题型:
| 金额/元 | 5 | 6 | 7 | 10 |
| 人数 | 2 | 3 | 2 | 1 |
| A、6.5元 | B、6元 |
| C、3.5元 | D、7元 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
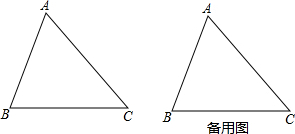 如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形?
如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com