
【题目】已知关于x的一元二次方程x2-2x+m-1=0.
(1)若此方程有两个不相等的实数根,求实数m的取值范围;
(2)当Rt△ABC的斜边长c=![]() ,且两直角边a和b恰好是这个方程的两个根时,求Rt△ABC的面积.
,且两直角边a和b恰好是这个方程的两个根时,求Rt△ABC的面积.
科目:初中数学 来源: 题型:
【题目】已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
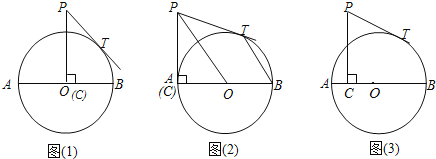
(1)如图1,当C点运动到O点时,求PT的长;
(2)如图2,当C点运动到A点时,连接PO、BT,求证:PO∥BT;
(3)如图3,设PT=y,AC=x,求y与x的解析式并求出y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣4,﹣3,﹣2,﹣1,0,1,3,4,5这九个数中,随机抽取一个数,记为a,则数a使关于x的不等式组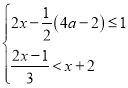 至少有四个整数解,且关于x的分式方程
至少有四个整数解,且关于x的分式方程![]() =1有非负整数解的概率是( )
=1有非负整数解的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图1,DE为△ABC的截线,截得四边形BCED,若∠BDE+∠C=180°,则称DE为△ABC边BC的逆平行线.如图2,已知△ABC中,AB=AC,过边AB上的点D作DE∥BC交AC于点E,过点E作边AB的逆平行线EF,交边BC于点F.
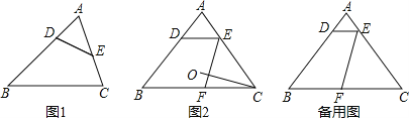
(1)求证:DE是边BC的逆平行线.
(2)点O是△ABC的外心,连接CO.求证:CO⊥FE.
(3)已知AB=5,BC=6,过点F作边AC的逆平行线FG,交边AB于点G.
①试探索AD为何值时,四边形AGFE的面积最大,并求出最大值;
②在①的条件下,比较AD+BG______AB大小关系.(“<、>或=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O ,交BC于点D,交CA的延长线于点E,连接AD,DE.
(1)求证:D是BC的中点
(2)若DE=3, AD=1,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,过点(﹣4,0),(0,﹣2).
(1)求抛物线的解析式和顶点坐标;
(2)当﹣4<x<4时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,直线
,直线![]() 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线![]() 交于点
交于点![]() .
.
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若![]() 的面积为6,求直线CD的表达式.
的面积为6,求直线CD的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com