
分析 (1)解两个函数解析式组成的方程组即可求解;
(2)过点P作PG⊥DF于点G,易证△PDG≌△ADE,点P作PH⊥CA于点H,可以证明H是AC的中点,则H的坐标即可求得,进而求得P的坐标,进而求得k的值;
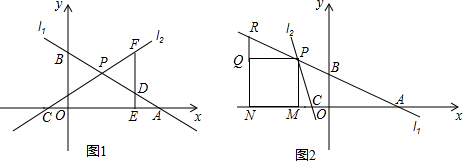
(3)Rt△PMC≌Rt△PQR,则RQ=MC,设NR=NC=a,则R(-a-2,a),代入y=-$\frac{1}{2}$x+3,求得a的值,设P(m,n),根据P在直线l1上和RQ=MC即可列方程组求解.
解答 解:(1)当k=1时,直线l2为y=x+2.
解方程组$\left\{\begin{array}{l}{y=x+2}\\{y=-\frac{1}{2}x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{8}{3}}\end{array}\right.$,
∴P($\frac{2}{3}$,$\frac{8}{3}$);
(2)当y=0时,kx+2k=0,
∵k≠0,
∴x=-2,
∴C(-2,0)则OC=2,
当y=0时,-$\frac{1}{2}$x+3=0,
∴x=6,
∴A(6,0),OA=6,
过点P作PG⊥DF于点G,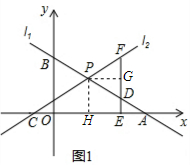 在△PDG和△ADE中,
在△PDG和△ADE中,
$\left\{\begin{array}{l}{∠PGD=∠AED}\\{∠PDG=∠ADE}\\{PD=AD}\end{array}\right.$,
∴△PDG≌△ADE,
得DE=DG=$\frac{1}{2}$DF,
∴PD=PF,
∴∠PFD=∠PDF
∵∠PFD+∠PCA=90°,∠PDF+∠PAC=90°
∴∠PCA=∠PAC,
∴PC=PA
过点P作PH⊥CA于点H,
∴CH=$\frac{1}{2}$CA=4,
∴OH=2,
当x=2时,y=-$\frac{1}{2}$×2+3=2代入y=kx+2k,得k=$\frac{1}{2}$;
(3)直角△PQR和直角△PMC中,
$\left\{\begin{array}{l}{PQ=PM}\\{PR=PC}\end{array}\right.$,
∴Rt△PMC≌Rt△PQR,
∴CM=RQ,
∴NR=NC,
设NR=NC=a,则R(-a-2,a),
代入y=-$\frac{1}{2}$x+3,
得-$\frac{1}{2}$(-a-2)+3=a,解得a=8,
设P(m,n),则$\left\{\begin{array}{l}{-\frac{1}{2}m+3=n}\\{-2-m=8-n}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{14}{3}}\\{n=\frac{16}{3}}\end{array}\right.$,
∴P(-$\frac{14}{3}$,$\frac{16}{3}$).
点评 本题是一次函数和全等三角形的判定的综合应用,正确作出辅助线,构造全等的三角形,证明H是AC的中点是解决本题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com