
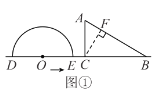
【题目】如图,半圆O的直径DE=12 cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=12 cm.半圆O以2 cm/s的速度自左向右运动,在运动过程中,点D,E始终在直线BC上.设运动时间为t s,当t=0时,半圆O在△ABC的左侧,OC=8 cm.
(1)当t=________s时,半圆O与AC所在直线第一次相切;点C到直线AB的距离为________.
(2)当t为何值时,直线AB与半圆O所在的圆相切?

【答案】(1)1,6 cm;(2)当t为4或16时,直线AB与半圆O所在的圆相切.
【解析】
(1)求出路程EC的长,即可以求时间t=1,作C到AB的距离CF,利用直角三角形中30°角所对的直角边是斜边的一半可以得:CF=6;
(2)根据C到AB的距离为6cm,圆的半径为6cm,所以O与C重合,即当O点运动到C点时,半圆O与△ABC的边AB相切,t=8÷2=4秒.
(1)∵DE=12 cm,
∴OE=OD=6 cm.
∵OC=8 cm,
∴EC=8-6=2(cm),
∴t=2÷2=1(s),
故当t=1时,半圆O与AC所在直线第一次相切.
如图①,过点C作CF⊥AB于点F.
在Rt△BCF中,∵∠ABC=30°,BC=12 cm,
∴CF=![]() BC=6 cm.
BC=6 cm.
故答案为1,6 cm.
(2)如图②,当半圆O在直线AB的左侧,与直线AB相切时,过点O作OM⊥AB于点M,则OM=6 cm.
∵∠ABC=30°,
∴OB=2OM=12 cm.
又∵BC=12 cm,
∴当点O与点C重合,即当点O运动到点C时,半圆O与△ABC的边AB相切,此时,点O运动了8 cm,运动时间t=8÷2=4.
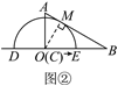
如图③,当半圆O所在的圆在直线AB的右侧与直线AB相切时,设切点为Q,则OQ⊥AB,OQ=6 cm.
在Rt△QOB中,∠OBQ=∠ABC=30°,则OB=2OQ=12 cm,此时点O运动了12+12+8=32(cm),运动时间t=32÷2=16.

综上所述,当t为4或16时,直线AB与半圆O所在的圆相切.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P 320千米处.

(1) 说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标;
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=2x2﹣mx+m﹣2,以下结论:①不论m取何值,抛物线总经过点(1,0);②抛物线与x轴一定有两个交点;③若m>6,抛物线交x轴于A、B两点,则AB>1;④抛物线的顶点在y=﹣2(x﹣1)2图象上.上述说法错误的序号是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(-2,-2),则k的值为 。
的图象上.若点A的坐标为(-2,-2),则k的值为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),点E是BC边上一点,把长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处.
(1)求点E、F的坐标;
(2)求AF所在直线的函数关系式;
(3)在x轴上求一点P,使△PAF成为以AF为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A,B都分成3等份的扇形区域,并在每一小区域内标上数字(如图所示),游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数,则甲获胜;若指针所指两个区域的数字之和为4的倍数,则乙获胜.如果指针落在分割线上,则需要重新转动转盘.请问这个游戏对甲、乙双方公平吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 、
、![]() 的中点,点
的中点,点![]() 为斜边
为斜边![]() 所在直线上一动点,且三角形
所在直线上一动点,且三角形![]() 为等腰直角三角形(
为等腰直角三角形(![]() ,
,![]() 、
、![]() 、
、![]() 呈逆时针).
呈逆时针).
![]() 如图
如图![]() 点
点![]() 在边
在边![]() 上,判断
上,判断![]() 和
和![]() 的数量和位置关系,请直接写出你的结论.
的数量和位置关系,请直接写出你的结论.
![]() 如图
如图![]() 点
点![]() 在
在![]() 点左侧时;如图
点左侧时;如图![]() ,点
,点![]() 在
在![]() 点右侧.其他条件不变,
点右侧.其他条件不变,![]() 中结论是否仍然成立,并选择图
中结论是否仍然成立,并选择图![]() 或图
或图![]() 的一种情况来说明理由.
的一种情况来说明理由.
![]() 在图
在图![]() 中若
中若![]() ,连接
,连接![]() ,请猜测
,请猜测![]() 与
与![]() 的数量关系,即
的数量关系,即![]() ________
________![]() .(用含
.(用含![]() 的三角函数的式子表示)
的三角函数的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com