

分析 (1)排列的数为自然数,最后的一个数是所在行数的平方,每行数的个数为1,3,5,…的奇数列,即可得到所求之数;
(2)由(1)得出第n行最后一数为n2,则第一个数为n2-2n+2,每行数由题意知每行数的个数为1,3,5,…的奇数列,故个数为2n-1;
(3)利用(2)的规律算出第21行的第一个数,最后一个数以及数的个数,利用求连续自然数的方法求得答案即可.
解答 解:(1)表中第8行的最后一个数是64,它是自然数8的平方,第8行共有15个数;
(2)用含n的代数式表示:第n行的第一个数是n2-2n+2,最后一个数是n2,第n行共有(2n-1)个数;
(3)第21行的第一个数为212-2×21+2=401,最后一个数是441,一共41个数,
数字和为(401+441)×41÷2=17261.
故答案为:64,8,15;n2-2n+2,n2,2n-1
点评 此题考查数字的变化规律,找出数字的排列规律和数字之间的运算规律,利用规律解决问题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,一架长2.5m的梯子,斜放在墙上,梯子的底部B离墙角O的距离是0.7m,当梯子的顶部A向下滑0.4m到A′时,梯子的底部向外移动0.8m.
如图,一架长2.5m的梯子,斜放在墙上,梯子的底部B离墙角O的距离是0.7m,当梯子的顶部A向下滑0.4m到A′时,梯子的底部向外移动0.8m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
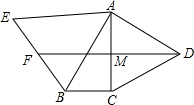 如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,F是BE的中点,DF交AC于M,试说明线段AM与MC相等的理由.
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,F是BE的中点,DF交AC于M,试说明线段AM与MC相等的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com