
 如图,一个正方体的棱长为2cm,一只蚂蚁欲从A点处沿正方体侧面到B点处吃食物,那么它需要爬行的最短路径的长是2$\sqrt{5}$cm.
如图,一个正方体的棱长为2cm,一只蚂蚁欲从A点处沿正方体侧面到B点处吃食物,那么它需要爬行的最短路径的长是2$\sqrt{5}$cm.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
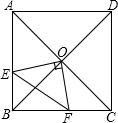 在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.
在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
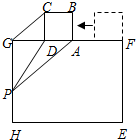 如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以lcm/s的速度沿FG方向移动,移动开始前点A与点F重合.在移动过程中,边 AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为lcm,矩形EFGH的边FG、GH的长分别为4cm、3cm.设正方形移动时间为x(s),线段GP的长为y (cm),其中0≤x≤2.5.
如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以lcm/s的速度沿FG方向移动,移动开始前点A与点F重合.在移动过程中,边 AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为lcm,矩形EFGH的边FG、GH的长分别为4cm、3cm.设正方形移动时间为x(s),线段GP的长为y (cm),其中0≤x≤2.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
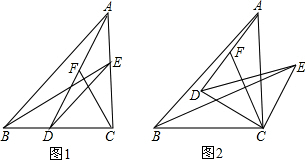
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
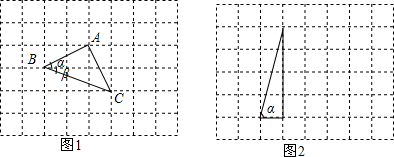
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com